
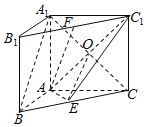
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1,且E,F分别是BC,B1C1中点.

(1)求证:A1B∥平面AEC1;
(2)求直线AF与平面AEC1所成角的正弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1) 连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 再证明
再证明![]() 即可.
即可.
(2) 作![]() 于
于![]() ,连接
,连接![]() ,再证明
,再证明![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角再求解即可.
所成角再求解即可.
证明:(1)连接A1C交AC1于点O,连接EO
∵ACC1A1为正方形,∴O为A1C中点,
又E为CB中点,∴EO为△A1BC的中位线,
∴EO∥A1B,
又EO平面AEC1,A1B平面AEC1,
∴A1B∥平面AEC1.
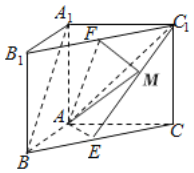
解:(2)作FM⊥EC1于M,连接AM,
∵AB=AC,E为BC的中点,
∴AE⊥BC,
又∵平面ABC⊥平面BCC1B1,且平面ABC⊥平面BCC1B1=BC,
AE平面ABC,∴AE⊥平面BCC1B1,
而AE平面AEC1,
∴平面AEC1⊥平面BCC1B1,∴FM⊥平面AEC1,
∴∠FAM即为直线AF与平面AEC1所成角,
设AB=AC=AA1=1,
则在Rt△AFM中,
在![]() 中,
中,![]() ,
,![]() ,
,![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
在![]() 中
中![]() ,
,![]() ,故
,故![]() ,
,
∴直线AF与平面AEC1所成角的正弦值sin∠FAM![]() .
.


科目:高中数学 来源: 题型:
【题目】如果函数f(x)=![]() x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
A. [-![]() ,
, ![]() ]
]
B. [-![]() ,
, ![]() ]
]
C. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
D. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为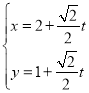 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据被墨迹污损不清(如图1),但甲得分的折线图完好(如图2),则下列结论错误的是( )
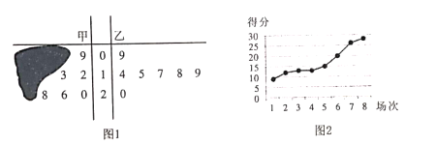
A.乙运动员得分的中位数是17,甲运动员得分的极差是19
B.甲运动员发挥的稳定性比乙运动员发挥的稳定性差
C.甲运动员得分有![]() 的叶集中在茎1上
的叶集中在茎1上
D.甲运动员得分的平均值一定比乙运动员得分的平均值低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,
,![]() .
.
(1)若集合![]() 含有三个元素,且
含有三个元素,且![]() ,这样的集合
,这样的集合![]() 有多少个?所有集合
有多少个?所有集合![]() 中个元素之和是多少?
中个元素之和是多少?
(2)若集合![]() 各含有三个元素,且
各含有三个元素,且![]() ,
,![]() ,
,![]() ,这样的集合
,这样的集合![]() 有多少种配对方式?
有多少种配对方式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com