
 某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.| 2π |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 12+12-2×1×1×cos2α |
| 2-co2α |
| 2π |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| π |
| 4 |
| 2 |
| 3 |
| 8 |


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
 定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输人a=2cos
定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输人a=2cos| 11π |
| 3 |
| A、-2 | B、0 | C、2 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
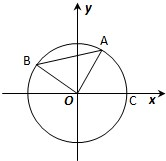 如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.
如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:
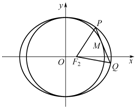 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com