
【题目】已知二次函数![]() .
.
(1)若![]() 为偶函数,求
为偶函数,求![]() 在
在![]() 上的值域;
上的值域;
(2)若![]() 的单调递减区间为
的单调递减区间为![]() ,求实数a构成的的集合;
,求实数a构成的的集合;
(3)若![]() 时,
时,![]() 的图像恒在直线
的图像恒在直线![]() 的上方,求实数a的取值范围.
的上方,求实数a的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据偶函数的对称性,求出![]() ,结合函数图像,即可求出
,结合函数图像,即可求出![]() 在
在![]() 上的值域;
上的值域;
(2)根据二次函数的单调性,确定对称轴满足的条件,即可得出结论;
(3)![]() 时,
时,![]() 的图像恒在直线
的图像恒在直线![]() 的上方,即
的上方,即![]() ,
,![]()
恒成立,分离参数,转化为参数与函数的最值关系,或设![]() ,分类讨论求出
,分类讨论求出![]() 时
时![]() 的最小值,进而解不等式
的最小值,进而解不等式![]() ,求出参数范围.
,求出参数范围.
(1)根据题意,函数![]() ,
,
为二次函数,其对称轴为![]() ,
,
若![]() 为偶函数,则
为偶函数,则![]() ,
,
解可得![]() ;则
;则![]() ,
,
又由![]() ,则有
,则有![]() ,
,
即函数![]() 的值域为
的值域为![]() ;
;
(2)根据题意,函数![]() ,
,
为二次函数,其对称轴为![]() ,
,
若![]() 在区间
在区间![]() 上是减函数,
上是减函数,
则![]() ,则
,则![]() ,所以a的取值范围是
,所以a的取值范围是![]() ;
;
(3)由题意知![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,
,
方法一:所以![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() ,
,
当且仅当![]() ,即
,即![]() 时取得“=”,
时取得“=”,
所以![]() ,解得
,解得![]() ,所以a的取值范围是
,所以a的取值范围是![]() .
.
方法二:令![]() ,
,
所以只需![]() ,对称轴为
,对称轴为![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,
解得![]() ,故
,故![]() ;
;
当![]() ,即
,即![]() 时,
时,
![]() ,
,
解得![]() ,故
,故![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() ,
,
解得![]() ,舍去;
,舍去;
综上所述,a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】现从某学校高二年级男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成![]() 组:第
组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,…,第
,…,第![]() 组
组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
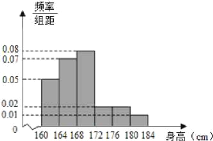
(1)估计这![]() 名男生身高的中位数和平均数;
名男生身高的中位数和平均数;
(2)求这![]() 名男生当中身高不低于
名男生当中身高不低于![]() 的人数,若在这
的人数,若在这![]() 名身高不低于
名身高不低于![]() 的男生中任意抽取
的男生中任意抽取![]() 人,求这
人,求这![]() 人身高之差不大于
人身高之差不大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某为台的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,将他们的候车时间(单位:分钟)作为样本分成
人,将他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 候车时间 | 人数 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求这![]() 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这![]() 名候车乘客中候车时间少于
名候车乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的![]() 人中随机抽取
人中随机抽取![]() 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足:
满足:![]() ,
,![]() 的最小值为1,且在
的最小值为1,且在![]() 轴上的截距为4.
轴上的截距为4.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若存在区间![]() ,使得函数
,使得函数![]() 的定义域和值域都是区间
的定义域和值域都是区间![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“不变区间”.试求函数
的“不变区间”.试求函数![]() 的不变区间;
的不变区间;
(3)若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某森林公园有一直角梯形区域ABCD,其四条边均为道路,AD∥BC,∠ADC=90°,AB=5千米,BC=8千米,CD=3千米.现甲、乙两管理员同时从![]() 地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.
地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.

(1)若甲、乙两管理员到达D的时间相差不超过15分钟,求乙的速度v的取值范围;
(2)已知对讲机有效通话的最大距离是5千米.若乙先到达D,且乙从A到D的过程中始终能用对讲机与甲保持有效通话,求乙的速度v的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ![]() )的周期为π,且图象上的一个最低点为M(
)的周期为π,且图象上的一个最低点为M(![]() ).
).
(1)求f(x)的解析式及单调递增区间;
(2)当x∈[0,![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
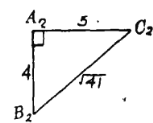
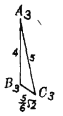
【题目】现有边长分别3,4,5的三角形两个,边长分别4,5,![]() 的三角形四个,边长分别为
的三角形四个,边长分别为![]() ,4,5的三角形六个.用上述三角形为面,可以拼成______个四面体.
,4,5的三角形六个.用上述三角形为面,可以拼成______个四面体.
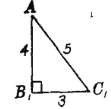
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com