
【题目】现从某学校高二年级男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成![]() 组:第
组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,…,第
,…,第![]() 组
组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
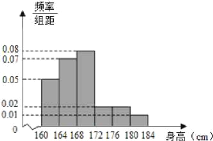
(1)估计这![]() 名男生身高的中位数和平均数;
名男生身高的中位数和平均数;
(2)求这![]() 名男生当中身高不低于
名男生当中身高不低于![]() 的人数,若在这
的人数,若在这![]() 名身高不低于
名身高不低于![]() 的男生中任意抽取
的男生中任意抽取![]() 人,求这
人,求这![]() 人身高之差不大于
人身高之差不大于![]() 的概率.
的概率.
【答案】(1)中位数为![]() .平均数为168.72(2)
.平均数为168.72(2)![]()
【解析】
(1)设中位数为![]() ,根据频率分布直方图可得
,根据频率分布直方图可得![]() ,解方程可求中位数;平均数
,解方程可求中位数;平均数![]() 每个小矩形的面积
每个小矩形的面积![]() 每个矩形底边中点横坐标之和.
每个矩形底边中点横坐标之和.
(2)根据频率分布直方图可得身高不低于![]() 的有
的有![]() 人,其中,低于
人,其中,低于![]() 的有
的有![]() 人,列举出从这
人,列举出从这![]() 个人中任意抽取
个人中任意抽取![]() 人的所有情况,然后再求出身高差不大于
人的所有情况,然后再求出身高差不大于![]() 的情况,利用古典概型的概率计算公式即可求解.
的情况,利用古典概型的概率计算公式即可求解.
解:(1)设这![]() 名男生身高的中位数为
名男生身高的中位数为![]() ,
,
因为第![]() 组
组![]() 的频率为
的频率为![]() ,第
,第![]() 组
组![]() 的频率为
的频率为![]() ,
,
所以![]() ,且
,且![]() ,
,
解得![]() 所以,这
所以,这![]() 名男生身高的中位数为
名男生身高的中位数为![]() .
.
平均数为![]()
(2)这![]() 名男生当中身高不低于
名男生当中身高不低于![]() 的有
的有![]() 人,
人,
其中,低于![]() 的有
的有![]() 人,记为
人,记为![]() ,另两个人记为
,另两个人记为![]() .
.
从这![]() 个人中任意抽取
个人中任意抽取![]() 人的所有情况列举如下:
人的所有情况列举如下:
![]()
![]()
![]()
![]()
![]() 共有
共有![]() 种情况,
种情况,
这![]() 人身高差不大于
人身高差不大于![]() 即
即![]() 人来自同一组,记为事件
人来自同一组,记为事件![]() ,共包含
,共包含![]() 个基本事件,
个基本事件,
则![]()


科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() (底面为正三角形,侧棱和底面垂直)的所有棱长都为2,
(底面为正三角形,侧棱和底面垂直)的所有棱长都为2,![]() 为
为![]() 的中点,O为
的中点,O为![]() 中点.
中点.
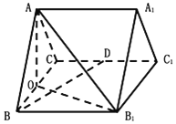
(1)求证:![]() 平面
平面![]() .
.
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)该小组发现种子的发芽数![]() (颗)与昼夜温差
(颗)与昼夜温差![]() (℃)呈线性相关关系,试求:线性回归方程
(℃)呈线性相关关系,试求:线性回归方程![]() .
.
(参考公式:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示样本均值.
表示样本均值.
参考数据:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是![]() ,现采用随机模拟的方法估计该运动员射击
,现采用随机模拟的方法估计该运动员射击![]() 次至多击中
次至多击中![]() 次的概率:先由计算器产生
次的概率:先由计算器产生![]() 到
到![]() 之间取整数值的随机数,指定
之间取整数值的随机数,指定![]() 、
、![]() 表示没有击中目标,
表示没有击中目标,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示击中目标,因为射击
表示击中目标,因为射击![]() 次,故以每
次,故以每![]() 个随机数为一组,代表射击
个随机数为一组,代表射击![]() 次的结果.经随机模拟产生了如下
次的结果.经随机模拟产生了如下![]() 组随机数:
组随机数:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
据此估计,射击运动员射击4次至多击中3次的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: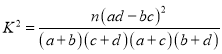 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W:![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)判断点A与以CD为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 为偶函数,求
为偶函数,求![]() 在
在![]() 上的值域;
上的值域;
(2)若![]() 的单调递减区间为
的单调递减区间为![]() ,求实数a构成的的集合;
,求实数a构成的的集合;
(3)若![]() 时,
时,![]() 的图像恒在直线
的图像恒在直线![]() 的上方,求实数a的取值范围.
的上方,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com