解:(I)由已知 点F (0,1)是线段MD的中点知A=2,∵S
△DMN =

S
△CDM=

=
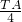
=

,∴T=

=

,ω=3.
∴函数f(x)=2sin(3x+φ),再由已知可得点M的坐标为(-

,0),由五点法作图可得 3(-

)+φ=0,∴φ=

.
(II)在△CDM中,∠DMN=α,∠CMN=β,则有 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.
而DC=2DM,故sinC=

sin∠DMC=

sin(α+β)=

sinαcosβ+

cosαsinβ=

cosαsinβ+

cosαsinβ=2cosαsinβ,
∴sinC=2cosαsinβ成立.
分析:(I)先由条件得到A=2,再由 S
△DMN=

S
△CDM=
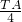
=

,求得 T=

=

,从而求得ω=3.求出点M的坐标为(-

,0),由五点法作图求得φ 值.
(II)在△CDM中,由题意可得 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.而DC=2DM,故sinC=

sin∠DMC=

sin(α+β),化简可得sinC=2cosαsinβ成立.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,三角函数的恒等变换及化简求值,属于中档题.

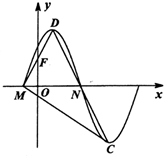 如图是函数f(x)=Asin(ωx+φ),A>0,ω>0,0<φ<
如图是函数f(x)=Asin(ωx+φ),A>0,ω>0,0<φ< 的部分图象,M,N是它与轴的两个交点,D,C分别为它的最高点和最低点,点F (0,1)是线段MD的中点,S△CDM=
的部分图象,M,N是它与轴的两个交点,D,C分别为它的最高点和最低点,点F (0,1)是线段MD的中点,S△CDM= .
. S△CDM=
S△CDM= =
=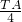 =
= ,∴T=
,∴T= =
= ,ω=3.
,ω=3. ,0),由五点法作图可得 3(-
,0),由五点法作图可得 3(- )+φ=0,∴φ=
)+φ=0,∴φ= .
. sin∠DMC=
sin∠DMC= sin(α+β)=
sin(α+β)= sinαcosβ+
sinαcosβ+ cosαsinβ=
cosαsinβ= cosαsinβ+
cosαsinβ+ cosαsinβ=2cosαsinβ,
cosαsinβ=2cosαsinβ, S△CDM=
S△CDM=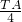 =
= ,求得 T=
,求得 T= =
= ,从而求得ω=3.求出点M的坐标为(-
,从而求得ω=3.求出点M的坐标为(- ,0),由五点法作图求得φ 值.
,0),由五点法作图求得φ 值. sin∠DMC=
sin∠DMC= sin(α+β),化简可得sinC=2cosαsinβ成立.
sin(α+β),化简可得sinC=2cosαsinβ成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案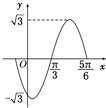 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π),x∈R的部分图象,则下列命题中,正确命题的序号为
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π),x∈R的部分图象,则下列命题中,正确命题的序号为
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象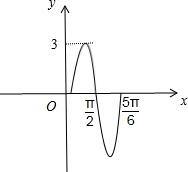 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤