
 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。 平面
平面 ;
; 的正切值的大小。(12分)
的正切值的大小。(12分)
 .
. 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,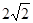 ,可得
,可得 ,于是
,于是 ,又
,又
 ,从而得到结论。
,从而得到结论。 于H,过点H作
于H,过点H作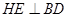 于E,
于E, 平面PAB,
平面PAB,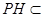 平面PAB,所以
平面PAB,所以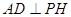 ,
, ,因而
,因而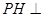 平面ABCD,
平面ABCD,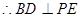 ,从而得到二面角的平面角
,从而得到二面角的平面角 是二面角P-BD-A的平面角,然后借助于三角形求解得到。
是二面角P-BD-A的平面角,然后借助于三角形求解得到。 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,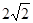 ,可得
,可得 ,
, ,……….2分,
,……….2分, ,又
,又 ….4分,
….4分, 平面PAB。……….6分,
平面PAB。……….6分, 于H,过点H作
于H,过点H作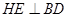 于E,
于E, 平面PAB,
平面PAB,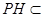 平面PAB,所以
平面PAB,所以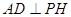 ,
, ,因而
,因而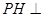 平面ABCD,
平面ABCD,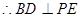 ,……….8分,
,……….8分, 是二面角P-BD-A的平面角。……….9分,
是二面角P-BD-A的平面角。……….9分,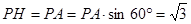 ,
, ,
, ,……….10分,
,……….10分, ~
~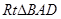 得
得 ,于是在
,于是在 中,
中, ,….11分,
,….11分, 。………….12分
。………….12分

科目:高中数学 来源:不详 题型:解答题
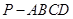 的底面为正方形,侧棱
的底面为正方形,侧棱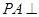 底面
底面 ,且
,且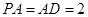 ,
,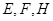 分别是线段
分别是线段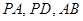 的中点.
的中点.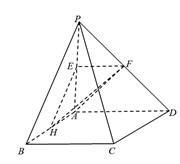
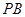 //平面
//平面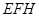 ;
;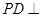 平面
平面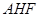 ;
;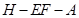 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若m∥n,m^a,则n^a | B.若m^a,mÌb,则a^b |
| C.若m^a,a∥b,则m^b | D.若a^b,mÌa,则m^b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com