

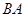 为
为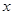 轴,
轴,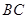 为
为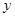 轴,
轴,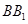 为
为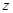 轴建立空间直角坐标系
轴建立空间直角坐标系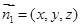 为平面
为平面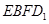 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,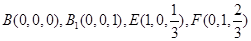
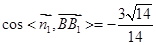 ,得到结论
,得到结论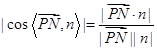 =
=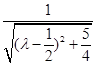 (*)
(*)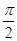 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=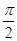 除外),
除外), 时,(sin θ)max=
时,(sin θ)max=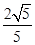 ,(tan θ)max=2
,(tan θ)max=2 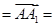 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),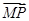 =(λ,-1,
=(λ,-1, ).
).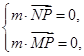 求出法向量,然后结合二面角得到解得λ=-
求出法向量,然后结合二面角得到解得λ=- .
. ,
, ,0),
,0),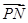 =(
=( -λ,
-λ,  ,-1),
,-1),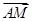 =(0,1,
=(0,1,  ).
).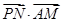 =(
=( -λ)×0+
-λ)×0+ ×1-1×
×1-1× =0,
=0, 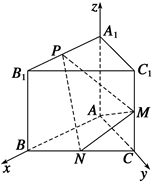
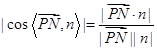 =
=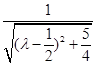 (*)
(*)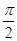 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=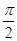 除外),
除外), 时,(sin θ)max=
时,(sin θ)max=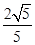 ,(tan θ)max=2 -----------6分
,(tan θ)max=2 -----------6分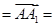 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),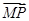 =(λ,-1,
=(λ,-1, ).
).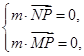
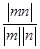 =
=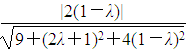 =
=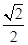 ,解得λ=-
,解得λ=- .
.

科目:高中数学 来源:不详 题型:解答题
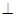 底面ABCD,
底面ABCD,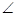 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.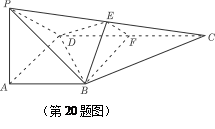
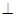 平面BEF;
平面BEF;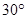 ,求k的取值范围.
,求k的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为正方形,
为正方形,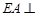 平面
平面 ,
,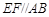 ,
,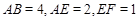 .
.
 在线段
在线段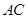 上,且满足
上,且满足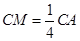 ,求证:
,求证: 平面
平面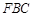 ;
;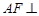 平面
平面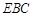 ;
; 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
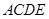 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
. 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;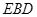 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.AC⊥BD |
| B.AC∥截面PQMN |
| C.AC=BD |
| D.异面直线PM与BD所成的角为45° |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是
是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是A.若m // ,? ,?   =" n" ,则m //n =" n" ,则m //n |
B.若m⊥ ?,n ?,n  ,m ⊥n ,则 ,m ⊥n ,则 ⊥ ⊥ ? ? ? ? |
C.若 // // ,m⊥ ,m⊥ ,n // ,n // ,则m⊥n ,则m⊥n |
D.若 ⊥ ⊥ , ,   =" m" ,m //n,则n // =" m" ,m //n,则n // |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com