练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．圆心在y轴上，且过点（3，1）的圆与x轴相切，则该圆的方程是（　　）
    A．x2+y2+10y=0B．x2+y2-10y=0C．x2+y2+10x=0D．x2+y2-10x=0

    分析 设出圆的圆心与半径，利用已知条件，求出圆的圆心与半径，即可写出圆的方程．

    解答 解：圆心在y轴上且过点（3，1）的圆与x轴相切，
    设圆的圆心（0，r），半径为r．
    则：$\sqrt{{（3-0）}^{2}+{（1-r）}^{2}}$=r．
    解得r=5．
    所求圆的方程为：x2+（y-5）2=25．即x2+y2-10y=0．
    故选：B．

    点评 本题考查圆的方程的求法，求出圆的圆心与半径是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

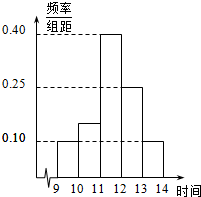    8．某商场在一日促销活动中，归该日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知11时至12时的销售额为10万元，则10时到11时的销售额为（单位：万元）（　　）
    A．2.5B．2.75C．3.25D．3.75

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知正四面体的各棱长都为$\sqrt{2}$，四个顶点都在同一球面上，则该球的表面积为3π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数$f（x）=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}，x∈R$．
    （ I）求$f（x）=-\frac{1}{2}$时x取值的集合；
    （ II）已知△ABC内角A，B，C的对边分别为a，b，c，且c=3，f（C）=0，若向量$\overrightarrow m=（1，sinA）与\overrightarrow n=（2，sinB）$共线，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知△ABC是单位圆O的内接三角形，AD是圆的直径，若满足$\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AC}•\overrightarrow{AD}={\overrightarrow{BC}^2}$，则$|\overrightarrow{BC}|$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=x|x-a|（a＞0）．
    （1）不等式f（x）≤1在[0，n]上恒成立，当n取得最大值时，求a的值；
    （2）在（1）的条件下．若对于任意的x∈R，不等式f（x+t）≥f（x）-t（t＞0）恒成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知f（x）=log4（4x-1）．
    （1）求f（x）的定义域；
    （2）讨论f（x）的单调性；
    （3）求f（x）在区间[$\frac{1}{2}$，2]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．设数列{an}的前n项和为Sn，且Sn2-2Sn-an•Sn+1=0，n∈N*．
    （1）求a1的值；
    （2）证明数列{$\frac{1}{{S}_{n}-1}$}是等差数列；
    （3）已知bn=$\frac{n+1}{n+2}$Sn（n∈N+），求数列{bn}列的前2015项之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列函数中，既不是奇函数，也不是偶函数的是（　　）
    A．y=x+sinxB．y=xsinxC．y=x+cosxD．y=xcosx

    查看答案和解析>>

    同步练习册答案