
分析 (I)利用三角函数恒等变换的应用化简函数解析式可得f(x)=$sin(2x-\frac{π}{6})-1$,可得$sin(2x-\frac{π}{6})=\frac{1}{2}$,解得x取值的集合.
(II)由题意可得$sin(2C-\frac{π}{6})=1$,结合C的范围,可求C的值,由m与n共线得sinB-2sinA=0,由正弦定理可得b=2a. ①由余弦定理,得$9={a^2}+{b^2}-2abcos\frac{π}{3}$. ②,解①②组成的方程组,即可得解.
解答 (本题满分为12分)
解:(I)$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x-1$=$sin(2x-\frac{π}{6})-1$…(3分)
由$f(x)=-\frac{1}{2}$得$sin(2x-\frac{π}{6})=\frac{1}{2}$,
故$2x-\frac{π}{6}=\frac{π}{6}+2kπ或2x-\frac{π}{6}=\frac{5π}{6}+2kπ,k∈Z$,
所以x取值的集合为:$\left\{{\left.x\right|x=\frac{π}{6}+kπ或x=\frac{π}{2}+kπ,k∈Z}\right\}$…(5分)
(II)∵$f(C)=sin(2C-\frac{π}{6})-1=0$,即$sin(2C-\frac{π}{6})=1$,
∵$0<C<π,-\frac{π}{6}<2C-\frac{π}{6}<\frac{11π}{6}$,
∴$2C-\frac{π}{6}=\frac{π}{2}$,
∴$C=\frac{π}{3}$…(6分)
∵m与n共线,∴sinB-2sinA=0,
由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,得b=2a. ①…(8分)
∵c=3,由余弦定理,得$9={a^2}+{b^2}-2abcos\frac{π}{3}$. ②…(10分)
解①②组成的方程组,得$\left\{\begin{array}{l}a=\sqrt{3}\\ b=2\sqrt{3}.\end{array}\right.$…(12分)
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质,考查了正弦定理,余弦定理,平面向量与共线向量的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,+∞) | C. | (-2,+∞) | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2+10y=0 | B. | x2+y2-10y=0 | C. | x2+y2+10x=0 | D. | x2+y2-10x=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
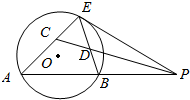 如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.
如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4} | D. | {2,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com