练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    （1）若，证明：；

    （2）若，且，求的取值范围；

    （3）若，且方程有个不同的根，求的取值范围.

    【答案】（1）证明见解析；（2）；（3）

    【解析】

    （1）由，可得，将等式两边分别代入解析式即可证明.

    （2）根据题意可得函数为增函数，只需在恒成立，分离参数即可求解.

    （3）利用导数确定函数的单调区间，作出函数的大致图像，数形结合即可求解.

    （1）当时，则，

    所以左边，

    右边

    ，即证.

    （2）由，，

    则函数在上单调递增，

    即在上恒成立，

    即在上恒成立，只需，

    设，由，所以，

    所以.

    （3）当时，

    则，

    令，解得或；

    令，解得，

    所以函数的单调递增区间为，，

    函数的单调递减区间为，

    且，，

    在同一坐标系中作出与的图像如图所示：

    方程有个不同的根，由图像可知：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2019年扬州市政府打算在如图所示的某“葫芦”形花坛中建一喷泉，该花坛的边界是两个半径为12米的圆弧围成，两圆心、之间的距离为米．在花坛中建矩形喷泉，四个顶点，，，均在圆弧上，于点．设.

    当 时,求喷泉的面积;

    (2)求为何值时，可使喷泉的面积最大?.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是正方形， 平面， // ， ， ， 为的中点．

    （1）求证： ；

    （2）求证： //平面；

    （3）求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三角形的面积为，其中，，为三角形的边长，为三角形内切圆的半径，则利用类比推理，可得出四面体的体积为（ ）

    A.

    B.

    C. ，（为四面体的高）

    D. ，（，，，分别为四面体的四个面的面积，为四面体内切球的半径）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）当时，若函数恰有一个零点，求的取值范围；

    （2）当时， 恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出如图数阵的表格形式，表格内是按某种规律排列成的有限个正整数.

    （1）记第一行的自左至右构成数列，是的前项和，试求的表达式；

    （2）记为第行与第列交点的数字，观察数阵，若，试求出的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解关于x的不等式

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆的中心在原点，焦点在轴上，长轴长是短轴长的2倍且经过点，平行于的直线在轴上的截距为，直线交椭圆于两个不同点．

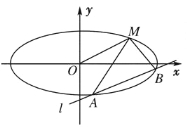
    （1）求椭圆的方程；

    （2）求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中.

    （1）讨论的单调性；

    （2）设函数，当时，若，，总有成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案