
分析 由题意知本题是一个古典概型,试验发生包含的事件数是36,求出满足条件的事件是直线ax+by=0与圆(x-2)2+y2=2无公共点的基本事件个数,代入古典概型概率公式得到结果.
解答 解:将一枚骰子先后抛掷两次得到的点数依次记为a,b,基本事件总数是36种,
∵直线ax+by=0与圆(x-2)2+y2=2无公共点,则有 $\frac{|2a|}{\sqrt{{a}^{2}{+b}^{2}}}$>$\sqrt{2}$⇒a>b,
∴满足该条件的基本事件有15种,
故所求概率为P=$\frac{15}{36}$=$\frac{5}{12}$.
故答案为:$\frac{5}{12}$.
点评 本题考查古典概型,考查对立事件的概率,考查简单直线与圆的位置关系,是一个综合题,本题解题的难点不是古典概型,而是题目中出现的其他的知识点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
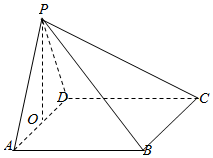 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD,O为棱AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD,O为棱AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{b-a+\frac{1}{c-b}}|≥2$ | B. | a3b+b3c+c3a≥a4+b4+c4 | ||
| C. | b2≥ac | D. | |b|-|a|≤|c|-|b| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com