
分析 (1)通过a=1化简二次函数,求出对称轴判断开口方向,然后求解值域;
(2)利用分段函数的单调性,结合二次函数的对称轴,以及函数值的关系,求解即可.
解答 解:(1)当a=1时,f(x)=x2+x+3.x∈[-1,1]对称轴$x=-\frac{1}{2}$,…(1分)
故${f_{min}}(x)=f(-\frac{1}{2})=\frac{11}{4}$,fmax(x)=f(1)=5…(3分)
函数f(x)的值域为$[\frac{11}{4},5]$…(4分)
(2)由已知可得f(x)在(-∞,0)时单调递减,
故对称轴$-\frac{4a-3}{2}≥0$即$a≤\frac{3}{4}$…(6分)
f(x)在[0,+∞)时单调递减,故即0<a<1…(7分)
又g(x)在R上递减,则f(0)≥g(0),即3a≥1,解得$a≥\frac{1}{3}$…(9分)
综上$\frac{1}{3}≤a≤\frac{3}{4}$…(10分)
点评 本题考查分段函数的应用,二次函数的性质的应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-∞,-2)∪(1,+∞) | C. | (1,+∞) | D. | (-∞,-1)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{5}{2}$) | B. | ($\frac{5}{2}$,+∞) | C. | (-∞,-1) | D. | (6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
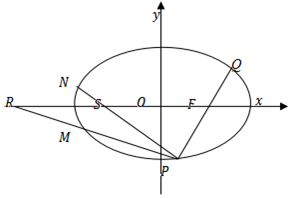 如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.
如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com