
| A. | $|{b-a+\frac{1}{c-b}}|≥2$ | B. | a3b+b3c+c3a≥a4+b4+c4 | ||
| C. | b2≥ac | D. | |b|-|a|≤|c|-|b| |
分析 本题是选择题,可以采用特值法与排除法结合,不妨取a,b,c分别为1,2,3,不难选出答案B.
解答 解:对于选择题,可以用特值法与排除法
设a=1,b=2,c=3
∴ab+bc+ca=11 a2+b2+c2=14
所以B不成立,故选B.
对于其他三个选项证明如下:
设等差数列的公差为d≠0
∴b-a=c-b=d∴|b-a+$\frac{1}{c-b}$|=|d+$\frac{1}{d}$|≥2,故A正确,
∵a,b,c成等差数列
∴2b=a+c≥2$\sqrt{ac}$,
∴b2≥ac,故C正确,
又|2b|=|a+c|≤|a|+|c|
∴|b|-|a|≤|c|-|b|,故D正确,
故选:B.
点评 本题旨在考查不等关系与不等式以及等差数列的性质,但本题是选择题,用特值法与排除法解决应该是应试的技巧,值得注意.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
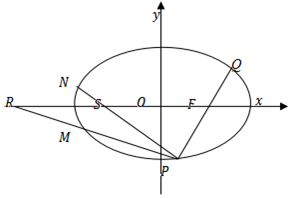 如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.
如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com