
【题目】已知函数f(x)=xlnx+2x﹣1.
(1)求f(x)的极值;
(2)若对任意的x>1,都有f(x)﹣k(x﹣1)>0(k∈Z)恒成立,求k的最大值.
【答案】(1)极小值为﹣e﹣3﹣1,无极大值;(2)最大值为4.
【解析】
(1)求导判断函数的单调性,由极值定义得解;(2)问题转化为![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,利用导数求函数
,利用导数求函数![]() 的范围,进而得到实数
的范围,进而得到实数![]() 的范围,由此得到答案.
的范围,由此得到答案.
(1)函数f(x)的定义域为(0,+∞),f′(x)=lnx+3,
令f′(x)=0,解得x=e﹣3,
当x∈(0,e﹣3)时,f′(x)<0,函数f(x)递减;
当x∈(e﹣3,+∞)时,f′(x)>0,函数f(x)递增;
故f(x)的极小值为f(e﹣3)=﹣e﹣3﹣1,无极大值;
(2)原式可化为![]() ,
,
令![]() ,则
,则![]() ,
,
令h(x)=x﹣2﹣lnx(x>1),则![]() ,
,
故h(x)在(1,+∞)上递增,
故存在唯一的x0∈(3,4),使得h(x0)=0,即lnx0=x0﹣2,
且当x∈(1,x0)时,h(x)<0,g′(x)<0,g(x)递减;
当x∈(x0,+∞)时,h(x)>0,g′(x)>0,g(x)递增;
故g(x)min=g(x0)=x0+1,
故k<x0+1∈(4,5),所以实数k的最大值为4.


科目:高中数学 来源: 题型:
【题目】过正四面体ABCD的顶点A作一个形状为等腰三角形的截面,且使截面与底面BCD所成的角为![]() ,这样的截面有( )
,这样的截面有( )
A.6个B.12个C.16个D.18个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家正积极推行垃圾分类工作,教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》.《通知》指出,到2020年底,各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查(每个受访者只能在问卷的4个活动中选择一个)如图是调查结果的统计图,以下结论正确的是( )
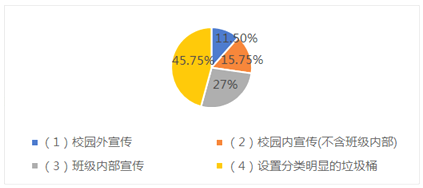
A.回答该问卷的受访者中,选择的(2)和(3)人数总和比选择(4)的人数多
B.回该问卷的受访者中,选择“校园外宣传”的人数不是最少的
C.回答该问卷的受访者中,选择(4)的人数比选择(2)的人数可能多30人
D.回答该问卷的总人数不可能是1000人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某校某班44名同学的某次考试的物理成绩y和数学成绩x的散点图:
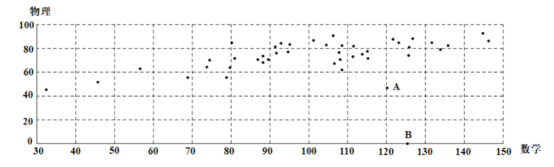
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计量的值:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() .y与x的相关系数
.y与x的相关系数![]() .
.
(1)若不剔除A、B两名考生的数据,用44数据作回归分析,设此时y与x的相关系数为![]() ,试判断
,试判断![]() 与r的大小关系,并说明理由;
与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到![]() ),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
附:回归方程![]() 中,
中, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(1)若曲线![]() 在
在![]() 处的切线也是抛物线
处的切线也是抛物线![]() 的切线,求
的切线,求![]() 的值;
的值;
(2)若对于任意![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,是否存在
时,是否存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数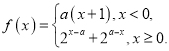 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com