
【题目】设函数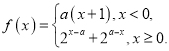 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
【答案】③④
【解析】
取![]() ,由一次函数的单调性和基本不等式,可得函数
,由一次函数的单调性和基本不等式,可得函数![]() 的值域,可判断①的正误;当
的值域,可判断①的正误;当![]() 时,可以否定②;考虑
时,可以否定②;考虑![]() 时,求得函数
时,求得函数![]() 的值域,即可判断③;当
的值域,即可判断③;当![]() 时,结合一次函数的单调性和基本不等式,以及函数
时,结合一次函数的单调性和基本不等式,以及函数![]() 的图象,即可判断④.综合可得出结论.
的图象,即可判断④.综合可得出结论.
对于①,可取![]() ,则
,则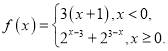 ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时,取得等号,
时,取得等号,
故![]() 时,
时,![]() 的值域为R,
的值域为R,
∴![]() ,
,![]() 都有解,故①错误;
都有解,故①错误;
对于②,当![]() 时,由于对于任意
时,由于对于任意![]() ,
,![]() 无解;
无解;
![]() 时,
时,![]() ,对任意的
,对任意的![]() ,至多有一个实数根,故②错误;
,至多有一个实数根,故②错误;
对于③,当![]() 时,
时,![]() 时,
时,![]() 单调递减,可得
单调递减,可得![]() ;
;
又![]() 时,
时,![]() ,即有
,即有![]() .
.
可得![]() ,则
,则![]() 的值域为
的值域为![]() ,
,
∴![]() ,
,![]() 都有解,故③正确;
都有解,故③正确;
对于④,当![]() 时,
时,![]() 时,
时,![]() 递增,可得
递增,可得![]() ;
;
当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时,取得等号,
时,取得等号,
由图象可得,当![]() 时,
时,![]() 有三解,故④正确.
有三解,故④正确.
故答案为:③④.



科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成3组派去三地执行公务(每地至少去1人),则不同的方案有( )种.
A.150B.180C.240D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.
表1
文本学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换 得到曲线E,直线
得到曲线E,直线 (t为参数)与曲线E交于A,B两点.
(t为参数)与曲线E交于A,B两点.
(1)设曲线C上任一点为![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲线E的直角坐标方程,并求出直线l被曲线E截得的弦AB长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂每天的固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为a元时,生产x件产品的销售收入为![]() (元),
(元),![]() 为每天生产x件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件a元进货后又以每件b元销售,
为每天生产x件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件a元进货后又以每件b元销售,![]() ,其中c为最高限价
,其中c为最高限价![]() ,
,![]() 为该产品畅销系数.据市场调查,
为该产品畅销系数.据市场调查,![]() 由当
由当![]() 是
是![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量x为多少时,平均利润![]() 取得最大值?并求出
取得最大值?并求出![]() 的最大值;
的最大值;
(2)求畅销系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求a与b的值.
,当厂家平均利润最大时,求a与b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com