
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
【答案】(1)分布列见解析,![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)抛掷5次的得分![]() 可能为
可能为![]() ,且正面向上和反面向上的概率相等,都为
,且正面向上和反面向上的概率相等,都为![]() ,所以得分
,所以得分![]() 的概率为
的概率为![]() ,即可得分布列和数学期望;
,即可得分布列和数学期望;
(2)令![]() 表示恰好得到
表示恰好得到![]() 分的概率,不出现
分的概率,不出现![]() 分的唯一情况是得到
分的唯一情况是得到![]() 分以后再掷出一次反面.,因为“不出现
分以后再掷出一次反面.,因为“不出现![]() 分”的概率是
分”的概率是![]() ,“恰好得到
,“恰好得到![]() 分”的概率是
分”的概率是![]() ,因为“掷一次出现反面”的概率是
,因为“掷一次出现反面”的概率是![]() ,所以有
,所以有![]() ,即
,即![]() ,所以
,所以![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,即求得恰好得到
为公比的等比数列,即求得恰好得到![]() 分的概率.
分的概率.
试题解析:(1)所抛5次得分![]() 的概率为
的概率为![]() ,
,
其分布列如下
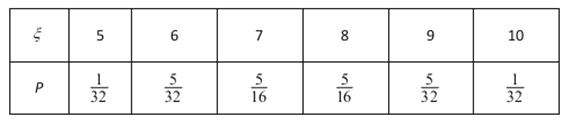
![]()
(2)令![]() 表示恰好得到
表示恰好得到![]() 分的概率,不出现
分的概率,不出现![]() 分的唯一情况是得到
分的唯一情况是得到![]() 分以后再掷出一次反面.
分以后再掷出一次反面.
因为“不出现![]() 分”的概率是
分”的概率是![]() ,“恰好得到
,“恰好得到![]() 分”的概率是
分”的概率是![]() ,
,
因为“掷一次出现反面”的概率是![]() ,所以有
,所以有![]() ,
,
即![]() .
.
于是![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列.
为公比的等比数列.
所以![]() ,即
,即![]() .
.
恰好得到![]() 分的概率是
分的概率是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对![]() 方格表中的小方格进行染色.使得每个被染色的小方格满足:与其相邻的小方格中最多只有一个被染色,其中两个小方格相邻是指它们有一条公共边.问:最多可以给多少个小方格染色?
方格表中的小方格进行染色.使得每个被染色的小方格满足:与其相邻的小方格中最多只有一个被染色,其中两个小方格相邻是指它们有一条公共边.问:最多可以给多少个小方格染色?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)请画出性别与休闲方式的![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.10的前提下,认为休闲方式与性别有关?
附: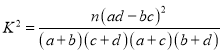 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且
,且![]() 时
时![]() ,甲,乙,丙,丁四位同学有下列结论:
,甲,乙,丙,丁四位同学有下列结论:
甲:![]() ;
;
乙:函数![]() 在
在![]() 上是增函数;
上是增函数;
丙:函数![]() 关于直线
关于直线![]() 对称;
对称;
丁:若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在
在![]() 上所有根之和为
上所有根之和为![]() 其中正确的是( ).
其中正确的是( ).
A. 甲,乙,丁 B. 乙,丙 C. 甲,乙,丙 D. 甲,丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数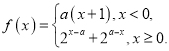 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com