
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且
,且![]() 时
时![]() ,甲,乙,丙,丁四位同学有下列结论:
,甲,乙,丙,丁四位同学有下列结论:
甲:![]() ;
;
乙:函数![]() 在
在![]() 上是增函数;
上是增函数;
丙:函数![]() 关于直线
关于直线![]() 对称;
对称;
丁:若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在
在![]() 上所有根之和为
上所有根之和为![]() 其中正确的是( ).
其中正确的是( ).
A. 甲,乙,丁 B. 乙,丙 C. 甲,乙,丙 D. 甲,丁
科目:高中数学 来源: 题型:
【题目】四川省阆中中学某部根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2018春季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高![]() 学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:
学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:

其中参加跑步类的人数所占频率为![]() ,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
![]() 1
1![]() 求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
![]() 2
2![]() 现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店销售某种商品,为了解该商品的月销量![]() (单位:千件)与月售价
(单位:千件)与月售价![]() (单位:元/件)之间的关系,对近几年的月销售量
(单位:元/件)之间的关系,对近几年的月销售量![]() 和月销售价
和月销售价![]() 数据进行了统计分析,得到了下面的散点图.
数据进行了统计分析,得到了下面的散点图.
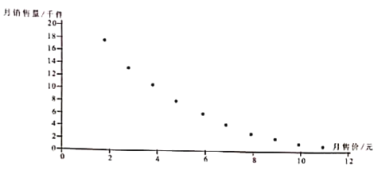
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为月销量
哪一个更适宜作为月销量![]() 关于月销售价
关于月销售价![]() 的回归方程类型?(给出判断即可,不需说明理由),并根据判断结果及表中数据,建立
的回归方程类型?(给出判断即可,不需说明理由),并根据判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)利用(1)中的结果回答问题:已知该商品的月销售额为![]() (单位:千元),当月销售量为何值时,商品的月销售额预报值最大?(月销售额=月销售量×当月售价)
(单位:千元),当月销售量为何值时,商品的月销售额预报值最大?(月销售额=月销售量×当月售价)
参考公式、参考数据及说明:
①对一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为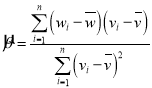 ,
,![]() .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 | -143.25 | -27.54 |
表中![]() ,
,![]() .
.
③计算时,所有的小数都精确到0.01,如![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由单位正方形组成的无限格阵的每个单位正方形内都写有一个整数.若每个方格内的整数等于其上方和左方与其相邻的两个方格内的整数之和,且存在一行![]() ,其中,所有方格内的数都是正整数.记
,其中,所有方格内的数都是正整数.记![]() 下面一行为
下面一行为![]() ,
,![]() 下面一行为
下面一行为![]() ,证明:对于每个正整数
,证明:对于每个正整数![]() ,
,![]() 上不能有
上不能有![]() 个方格内的整数都是0.
个方格内的整数都是0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以原点为极点,
(t为参数),以原点为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线![]() 关于
关于![]() 对称.
对称.
(1)求![]() 极坐标方程,
极坐标方程,![]() 直角坐标方程;
直角坐标方程;
(2)将![]() 向左平移4个单位长度,按照
向左平移4个单位长度,按照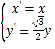 变换得到
变换得到![]() 与两坐标轴交于
与两坐标轴交于![]() 两点,
两点,![]() 为
为![]() 上任一点,求
上任一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com