
【题目】已知函数![]() 满足
满足![]() ,对于任意
,对于任意![]() ,且
,且![]() .令
.令![]() .
.
(1)求函数![]() 解析式;
解析式;
(2)探求函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1)![]() ;(2)当
;(2)当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点,当
上有一个零点,当![]() 时,函数
时,函数![]() 在
在![]() 上没有零点.
上没有零点.
【解析】
试题分析:(1)由![]() ,得
,得![]() ,由
,由![]() 可知
可知![]() ,以及任意
,以及任意![]() ,可得
,可得![]()
![]() ,综合求得
,综合求得![]() ;(2)
;(2)![]() 是一分段函数,先讨论对称轴
是一分段函数,先讨论对称轴![]() 和
和![]() 与绝对值零点
与绝对值零点![]() 的大小,再在每种情况下讨论绝对值零点和区间端点的大小关系进行分类讨论.
的大小,再在每种情况下讨论绝对值零点和区间端点的大小关系进行分类讨论.
试题解析:(1)由![]() ,得
,得![]() ,由
,由![]() 可知
可知![]() , 所以
, 所以![]() ,又对于任意
,又对于任意![]() ,
,![]() ,即
,即![]() 都成立, 所以
都成立, 所以![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
(2) ,
,
若![]() ,
,![]() ,其对称轴为
,其对称轴为![]() ,当
,当![]() ,即
,即![]() 时,函数在
时,函数在![]() 上为增函数; 当
上为增函数; 当![]() ,即
,即![]() 时,函数在
时,函数在![]() 上为减函数, 在
上为减函数, 在![]() 上为增函数;若
上为增函数;若![]() ,
,![]() 其对称轴为
其对称轴为![]() ,此时
,此时![]() , 所以函数在
, 所以函数在![]() 上为减函数, 在
上为减函数, 在![]() 上为增函数, 且
上为增函数, 且![]()
![]() ,所以函数
,所以函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时 ,
时 , ,没有零点;当
,没有零点;当![]() 时,函数
时,函数![]() 在
在![]() 上为增函数, 在
上为增函数, 在![]() 上为减函数,且
上为减函数,且![]()
![]() ,若
,若![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上没有零点, 若
上没有零点, 若![]() ,即
,即![]() 时, 函数
时, 函数![]() 在
在![]() 上有一个零点.综上得, 当
上有一个零点.综上得, 当![]() 或
或![]() 时函数
时函数
![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 上没有零点.
上没有零点.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
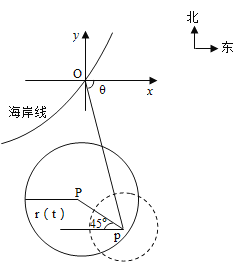
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300km的海面
方向300km的海面![]() 处,并以20km/h的速度向西偏北
处,并以20km/h的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-![]() sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率
的离心率![]() ,长轴长为4.
,长轴长为4.

(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 与直线
与直线![]() 交与点
交与点![]() ,且
,且![]() .求证:点
.求证:点![]() 在定直线上,并求出定直线方程.
在定直线上,并求出定直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(3)记集合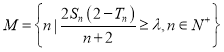 ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②平行于同一平面的两条直线相互平行;
③若一条直线平行于一个平面内的无数条直线,那么这条直线平行于这个平面;
④若一条直线垂直于一个平面内的任一条直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com