
【题目】设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=﹣b,其中常数a,b∈R. (Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程.
(Ⅱ)设g(x)=f′(x)e﹣x . 求函数g(x)的极值.
【答案】解:(Ⅰ)∵f(x)=x3+ax2+bx+1∴f'(x)=3x2+2ax+b.令x=1,得f'(1)=3+2a+b=2a,解得b=﹣3 令x=2,得f'(2)=12+4a+b=﹣b,因此12+4a+b=﹣b,解得a=﹣ ![]() ,因此f(x)=x3﹣
,因此f(x)=x3﹣![]() x2﹣3x+1
x2﹣3x+1
∴f(1)=﹣ ![]() ,
,
又∵f'(1)=2×(﹣ ![]() )=﹣3,
)=﹣3,
故曲线在点(1,f(1))处的切线方程为y﹣(﹣ ![]() )=﹣3(x﹣1),即6x+2y﹣1=0.
)=﹣3(x﹣1),即6x+2y﹣1=0.
(Ⅱ)由(I)知g(x)=(3x2﹣3x﹣3)e﹣x
从而有g'(x)=(﹣3x2+9x)e﹣x
令g'(x)=0,则x=0或x=3
∵当x∈(﹣∞,0)时,g'(x)<0,
当x∈(0,3)时,g'(x)>0,
当x∈(3,+∞)时,g'(x)<0,
∴g(x)=(3x2﹣3x﹣3)e﹣x在x=0时取极小值g(0)=﹣3,在x=3时取极大值g(3)=15e﹣3
【解析】(Ⅰ)根据已知中f(x)=x3+ax2+bx+1,我们根据求函数导函数的公式,易求出导数f'(x),结合f'(1)=2a,f'(2)=﹣b,计算出参数a,b的值,然后求出f(1)及f'(1)的值,然后代入点斜式方程,即可得到曲线y=f(x)在点(1,f(1))处的切线方程.(Ⅱ)根据g(x)=f′(x)e﹣1求出函数g(x)的解析式,然后求出g(x)的导数g'(x)的解析式,求出导函数零点后,利用零点分段法,分类讨论后,即可得到函数g(x)的极值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 ![]() 和
和 ![]() .现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
(Ⅱ)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( ) 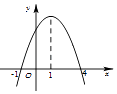
A.在x=﹣1处取得极大值
B.在区间[﹣1,4]上是增函数
C.在x=1处取得极大值
D.在区间[1,+∞)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:

参考数据: ![]() .参考公式:
.参考公式: ![]()

如果由资料知y对x呈线性相关关系.试求:
(1)![]() (2)线性回归方程
(2)线性回归方程![]()
(3)估计使用10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com