
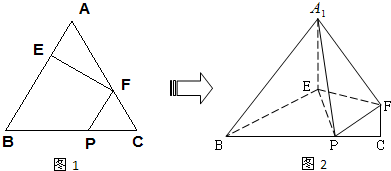
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
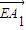 ,平面A1BP的法向量
,平面A1BP的法向量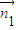 ,利用
,利用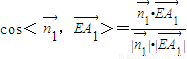 ,求直线A1E与平面A1BP所成角的大小.
,求直线A1E与平面A1BP所成角的大小.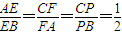 ,AF=AD=2,又∠A=60°,△ADF为正三角形.
,AF=AD=2,又∠A=60°,△ADF为正三角形.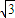 ,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.
,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.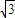 ,0),
,0),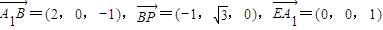
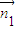 =(x,y,z),
=(x,y,z),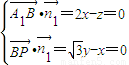
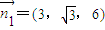 .
.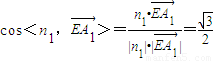
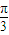 .
.

科目:高中数学 来源: 题型:
| AE |
| EB |
| CF |
| FA |
| CP |
| PB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小;
(3)求二面角B—A1P—F的大小(用反三角函数值表示).

(1) (2)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州地区七校联考高二(上)期中数学试卷(解析版) 题型:解答题
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
查看答案和解析>>
科目:高中数学 来源:2008年江苏省扬州中学高考数学四模试卷(解析版) 题型:解答题
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com