
)为了了解中学生的身高情况,对某校中学生同年龄的若干名女生的身高进行了测量,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6(单位:cm)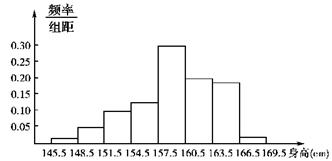
(1)参加这次测试的学生人数是多少?
(2)身高在哪个范围内的学生人数最多?这一范围内的人数是多少?
(3)如果本次测试身高在154.5 cm以上的为良好,试估计该校学生身高良好率是多少?
科目:高中数学 来源: 题型:解答题
(本小题满分13分)某同学大学毕业后在一家公司上班,工作年限 和年收入
和年收入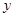 (万元),有以下的统计数据:
(万元),有以下的统计数据:
 | 3 | 4 | 5 | 6 |
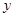 | 2.5 | 3 | 4 | 4.5 |
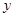 关于
关于 的线性回归方程
的线性回归方程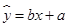 ;
;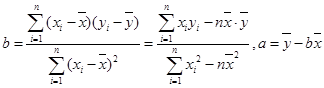 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某汽车厂生产A、B两类轿车,每类轿车均有舒适型和标准型两种,某月的产量如下表:
按分层抽样的方法在该月生产的轿车中抽取50辆,其中A类轿车20辆。
(I)求x的值;
(II)用分层抽样的方法在B类轿车中抽取一个容量为6的样本,从样本中任意取2辆,求至少有一辆舒适轿车的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在研究色盲与性别的关系调查中,调查了男性480人,其中有38有患色盲,调查的520个女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组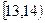 ,第二组
,第二组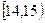 ……第五组
……第五组 ,如图是按上述分组方法
,如图是按上述分组方法 得到的频率分布直方图.
得到的频率分布直方图.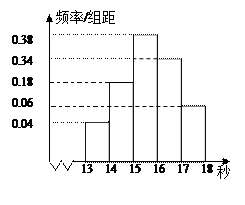
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
( II )根据有关规定,成绩小于16秒为达标.
(ⅰ)用样本估计总体,某班有学生45人,设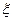 为达标人数,求
为达标人数,求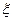 的数学期望与方差.
的数学期望与方差.
(ⅱ)如果男女生使用相同的达标标准,则男女
生达标情况如下表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 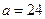 | 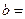 ______ ______ | _____ |
| 不达标 | 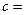 _____ _____ | 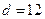 | _____ |
| 合计 | ______ | ______ |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如下: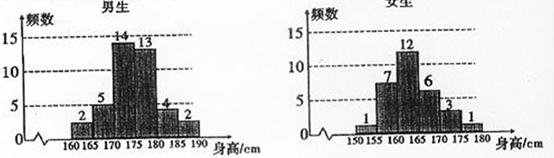
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。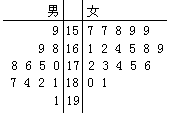
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用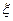 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出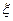 的分布列,并求
的分布列,并求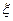 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)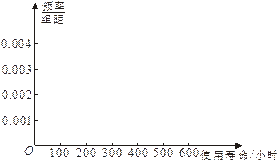
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
| 分组 | 频数 | 频率 |
| 100~200 | | |
| 200~300 | | |
| 300~400 | | |
| 400~500 | | |
| 500~600 | | |
| 合计 | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。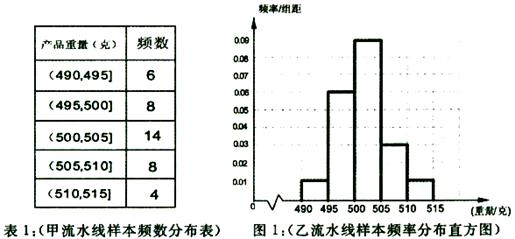 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| | 甲流水线 | 乙流水线 | 合 计 |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | | | n= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com