
(本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组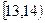 ,第二组
,第二组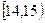 ……第五组
……第五组 ,如图是按上述分组方法
,如图是按上述分组方法 得到的频率分布直方图.
得到的频率分布直方图.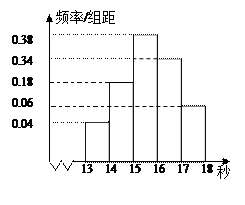
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
( II )根据有关规定,成绩小于16秒为达标.
(ⅰ)用样本估计总体,某班有学生45人,设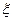 为达标人数,求
为达标人数,求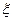 的数学期望与方差.
的数学期望与方差.
(ⅱ)如果男女生使用相同的达标标准,则男女
生达标情况如下表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 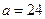 | 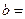 ______ ______ | _____ |
| 不达标 | 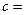 _____ _____ | 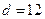 | _____ |
| 合计 | ______ | ______ |  |
科目:高中数学 来源: 题型:解答题
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,如图所示茎叶图,根据茎叶图问: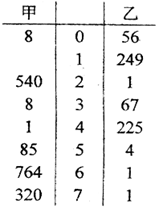
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在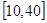 间的频率是多少?
间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分).以下是粤西地区某县搜集到的新房屋的销售价格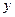 和
和 房屋的面积
房屋的面积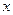 的数据:
的数据: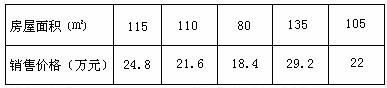
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为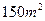 时的销售价格。
时的销售价格。
参考公式: 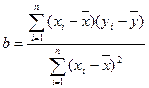 ,
,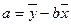
参考数据: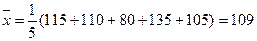 ,
,
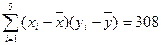 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
)为了了解中学生的身高情况,对某校中学生同年龄的若干名女生的身高进行了测量,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6(单位:cm)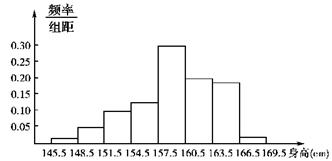
(1)参加这次测试的学生人数是多少?
(2)身高在哪个范围内的学生人数最多?这一范围内的人数是多少?
(3)如果本次测试身高在154.5 cm以上的为良好,试估计该校学生身高良好率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
有一个容量为50的样本,数据的 分组及各组的频数如下 3;
3;  8;
8; 9;
9; 11;
11; 10;
10;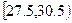 5;
5; 4.
4.
(1)列频率分布表
(2)画出频率分布直方图
(3)根据频率分布直方图估计数据落在 的概率是多少
的概率是多少
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(本小题12分)
某车间为了规定工时定额,需要 确定加工零件所花费的时间,为此作了四次试验如下:
确定加工零件所花费的时间,为此作了四次试验如下:
零件的个数 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
 点图;
点图;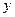 关于
关于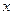 的线性回归方程
的线性回归方程 ;
; ,
,
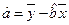
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图如图。
(1)求居民月收入在 的频率;(2)根据频率分布直方图算出样本数据的
的频率;(2)根据频率分布直方图算出样本数据的
中位数;(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中分层抽样方法抽出100人作进一步分析,
则月收入在 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)
某种产品的广告费支出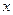 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
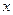 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,是总体的一样本频率分布直方图,且在[15,18)内频数为8。
(1)求样本容量;
(2)若在[12,15)内小矩形面积为0.06,求在[12,15)内的频数;
(3)求样本[18,33]内的频率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com