
(本小题13分)如图,棱锥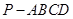 的底面
的底面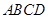 是矩形,
是矩形,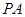 ⊥平面
⊥平面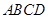 ,
,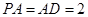 ,
,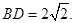
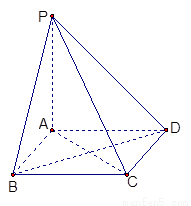
(1)求证: ⊥平面
⊥平面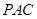 ;
;
(2)求二面角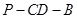 的大小;
的大小;
(3)求点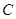 到平面
到平面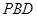 的距离.
的距离.
(1)见解析;(2)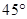 ;(3)
;(3)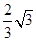
【解析】
试题分析:(方法一)证明:(1)在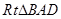 中,
中,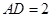 ,
,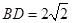 ,
,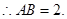
所以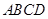 为正方形,因此
为正方形,因此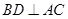 . ∵
. ∵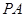 ⊥平面
⊥平面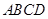 ,
,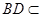 平面
平面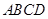 ,
,
∴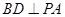 .又∵
.又∵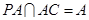 , ∴
, ∴ ⊥平面
⊥平面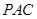 . ……4分
. ……4分
(2)解:由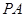 ⊥平面
⊥平面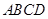 ,知
,知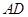 为
为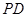 在平面
在平面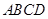 内的射影,
内的射影,
又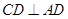 ,∴
,∴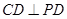 ,知
,知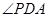 为二面角
为二面角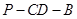 的平面角.
的平面角.
又∵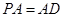 ,∴
,∴ .
……9分
.
……9分
(3)∵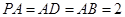 ,∴
,∴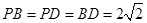 ,
,
设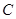 到面
到面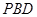 的距离为
的距离为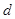 ,
,
由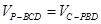 ,有
,有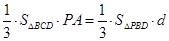 ,
,
即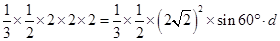 ,
,
得 .
……14分
.
……14分
(方法二)证明:(Ⅰ)建立如图所示的直角坐标系,

则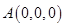 、
、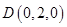 、
、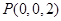 .
.
在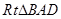 中,
中,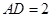 ,
,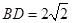 ,
,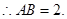 ∴
∴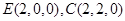 ,
,
∴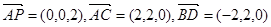 ∵
∵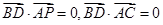 ,
,
即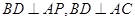 ,又∵
,又∵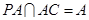 , ∴
, ∴ ⊥平面
⊥平面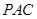 . ……4分
. ……4分
解:(2)由(Ⅰ)得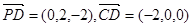 .
.
设平面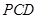 的法向量为
的法向量为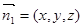 ,则
,则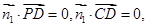
即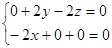 ,∴
,∴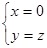 故平面
故平面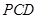 的法向量可取为
的法向量可取为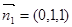
∵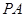 ⊥平面
⊥平面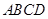 ,∴
,∴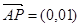 为平面
为平面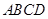 的法向量.
的法向量.
设二面角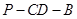 的大小为
的大小为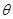 ,依题意可得
,依题意可得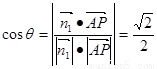 ,
,
∴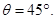 ……9分
……9分
(3)由(Ⅰ)得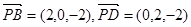 ,
,
设平面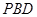 的法向量为
的法向量为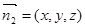 ,
,
则 ,即
,即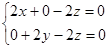 ,∴
,∴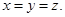 ,
,
故平面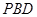 的法向量可取为
的法向量可取为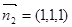 .
.
∵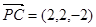 ,∴
,∴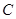 到面
到面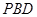 的距离为
的距离为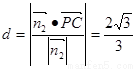 .
……14分
.
……14分
考点:本小题主要考查空间中线面垂直的证明、二面角以及点到平面的距离的求法,考查学生的空间想象能力、分析问题、解决问题的能力和运算能力.
点评:解决空间中的平行、垂直以及距离等问题,有传统方法和向量方法两种方法,用传统方法时,要注意紧扣定理,把符合定理的条件都列出来;用向量方法时,运算量较大,要仔细、快速进行.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2014届湖北武汉部分重点中学高二上学期期末考试文科数学卷(解析版) 题型:解答题
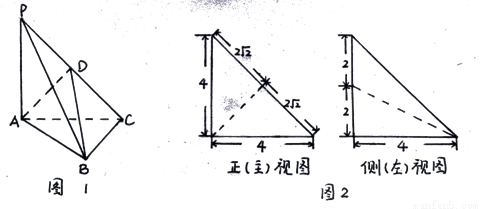
(本小题13分)如图1,在三棱锥P—ABC中, 平面ABC,
平面ABC, ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
(1)证明: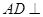 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在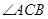 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得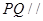 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
查看答案和解析>>
科目:高中数学 来源:2014届安徽宿松县复兴中学高一第二学期第三次月考数学试卷(解析版) 题型:解答题
(本小题13分)
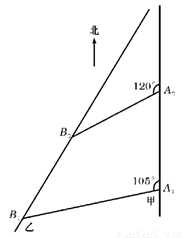
如图,甲船以每小时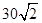 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于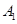 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西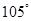 的方向
的方向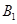 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达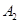 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西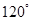 方向的
方向的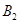 处,此时两船相距
处,此时两船相距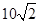 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区示范校高三第二学期综合练习数学文卷 题型:解答题
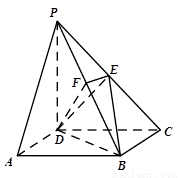
(本小题13分)如图,在四棱锥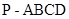 中,
中,
底面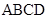 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面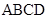 ,
,
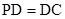 ,
,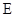 是
是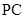 的中点,作
的中点,作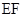 ⊥
⊥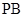 交
交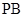 于点
于点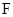 .
.
(1)证明: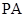 ∥平面
∥平面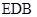 ;
;
(2)证明: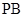 ⊥平面
⊥平面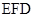 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com