
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用正弦定理化简易得![]() ,进而得到
,进而得到![]() ,由正弦定理即可求
,由正弦定理即可求![]() ;(2)根据
;(2)根据![]() 的面积为
的面积为![]() 和(1)中的
和(1)中的![]() ,易得
,易得![]() 结合余弦定理即可求得
结合余弦定理即可求得![]() .
.
试题解析:(1)由正弦定理得:![]() ,……………………1分
,……………………1分
即![]() ,……………………………………………………2分
,……………………………………………………2分
∴![]() ,……………………………………3分
,……………………………………3分
∵![]() ,∴
,∴![]() ,则
,则![]() ,………………………………………………5分
,………………………………………………5分
∵![]() ,∴由正弦定理得:
,∴由正弦定理得:![]() .………………………………6分
.………………………………6分
(2)∵![]() 的面积为
的面积为![]() ,
,
∴![]() ,得
,得![]() ,…………………………………………………………7分
,…………………………………………………………7分
∵![]() ,∴
,∴![]() ,…………………………………………9分
,…………………………………………9分
∴![]() ,即
,即![]() ,……………………………………11分
,……………………………………11分
∵![]() ,∴
,∴![]() .…………………………………………………………12分
.…………………………………………………………12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(1)已知椭圆方程为![]() ,点
,点![]() .
.
i.若关于原点对称的两点![]() 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
ii.若关于原点对称的两点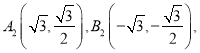 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
(2)根据上题结论探究:若![]() 是椭圆
是椭圆![]() 上关于原点对称的两点,点
上关于原点对称的两点,点![]() 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线![]() 的斜率都存在,并分别记为
的斜率都存在,并分别记为![]() ,试猜想
,试猜想![]() 的值,并加以证明.
的值,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),现以原点为极点,
为参数),现以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上是否存在一点
上是否存在一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小?若存在,求出距离的最小值及点
的距离最小?若存在,求出距离的最小值及点![]() 的直角坐标;若不存在,请说明理由.
的直角坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3-![]() x2+1(xR),其中a>0.
x2+1(xR),其中a>0.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市决定在其经济开发区一块区域进行商业地产开发,截止2015年底共投资![]() 百万元用于餐饮业和服装业,2016年初正式营业,经过专业经济师预算,从2016年初至2019年底的四年间,在餐饮业利润为该业务投资额的
百万元用于餐饮业和服装业,2016年初正式营业,经过专业经济师预算,从2016年初至2019年底的四年间,在餐饮业利润为该业务投资额的![]() ,在服装业可获利该业务投资额的算术平方根.
,在服装业可获利该业务投资额的算术平方根.
(1)该市投资资金应如何分配,才能使这四年总的预期利润最大?
(2)假设自2017年起,该市决定对所投资的区域设施进行维护保养,同时发放员工奖金,方案如下:2017年维护保养费用![]() 百万元,以后每年比上一年增加
百万元,以后每年比上一年增加![]() 百万元;2017年发放员工奖金共计
百万元;2017年发放员工奖金共计![]() 百万元,以后每年的奖金比上一年增加
百万元,以后每年的奖金比上一年增加![]() .若该市投资成功的标准是:从2016年初到2019的底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的
.若该市投资成功的标准是:从2016年初到2019的底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的![]() ,问该市投资是否成功?
,问该市投资是否成功?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga![]() (其中a>0,且a≠1).
(其中a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性并给出证明;
(3)若x∈![]() 时,函数f(x)的值域是[0,1],求实数a的值.
时,函数f(x)的值域是[0,1],求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
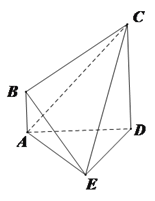
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com