分析:(1)以A为坐标原点,建立空间坐标系,设F(0,y,a),求出FD,B1E对应的向量,进而由FD∥B1E和向量平行的充要条件,可求出y值,进而判断出F点的位置;
(2)求出直线A1C与DE的方向向量,代入向量夹角公式,可得直线A1C与DE所成的角:
(3)设出平面B1ED的法向量及直线AD的方向向量,代入向量夹角公式,可得直线AD与平面B1ED所成的角.
解答: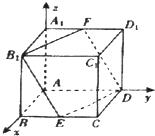
解:(1)建立如图所示的空间坐标系.
由正方体的性质,有B
1F∥ED,B
1E∥FD.
设F(0,y,a)
则
=(0,a-y,-a),=(0,,-a),
由FD∥B
1E得
a-y=,即
y=,
∴F为A
1D
2的中点.
(2)
=(a,a,-a),=(a,-,0),
∴
cos(,)===.
∴A
1C与DE所成的角
arccos.
(3)设平面B
1ED的法向量为
=(x,y,z),
则由
⊥,⊥得,
⇒⇒=(x,2x,x)取x=1,得
=(1,2,1),
又
=(0,a,0),
∴
cos(n,)==,
∴直线AD与平面B
1ED所成的角为
arccos.
点评:本题考查的知识点是直线与平面夹角问题,异面直线的夹角问题,其中建立空间坐标系,将直线夹角和线面夹角问题转化为向量夹角问题是解答的关键.

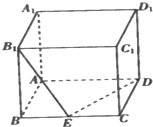 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,平面B1交A1D1于F.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,平面B1交A1D1于F. 解:(1)建立如图所示的空间坐标系.
解:(1)建立如图所示的空间坐标系.

![]() ,AG=
,AG=![]() ,给出下列四个命题:①AC⊥BD,②FG=
,给出下列四个命题:①AC⊥BD,②FG=![]() ,③侧面与底面所成二面角的余弦值为
,③侧面与底面所成二面角的余弦值为![]() ,④
,④![]() ,其中真命题的序号是( )
,其中真命题的序号是( )




