
设数列 的前n项和为
的前n项和为 ,且
,且 (
( ).
).
(1)求 ,
, ,
, ,
, 的值;
的值;
(2)猜想 的表达式,并加以证明。
的表达式,并加以证明。
(1)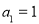 ,
,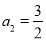 ,
,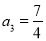 ,
,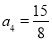 ; (2)猜想
; (2)猜想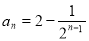 (
(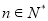 ),证明见解析.
),证明见解析.
【解析】
试题分析:(1)由条件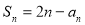 ,当
,当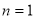 时,有
时,有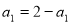 ,解得
,解得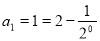 ,同理当
,同理当 分别取2,3,4可得
分别取2,3,4可得 ,
,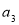 ,
,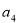 的值;(2)由(1)中前四项的值可猜想
的值;(2)由(1)中前四项的值可猜想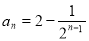 ,由
,由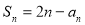 得
得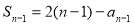 ,两式相减并化为
,两式相减并化为 ,则
,则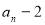 是等比数列,求出通项公式,可得
是等比数列,求出通项公式,可得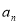 的通项公式.
的通项公式.
【解析】
(1)因为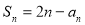 ,
,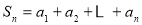 ,
,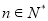 (1分)
(1分)
所以,当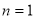 时,有
时,有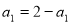 ,解得
,解得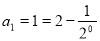 ; (2分)
; (2分)
当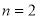 时,有
时,有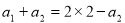 ,解得
,解得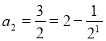 ; (3分)
; (3分)
当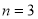 时,有
时,有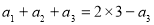 ,解得
,解得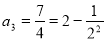 ; (4分)
; (4分)
当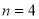 时,有
时,有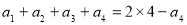 ,解得
,解得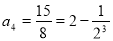 .(5分)
.(5分)
(2)猜想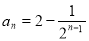 (
(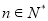 ) (9分)
) (9分)
方法一:
由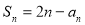 (
(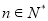 ),得
),得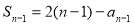 (
(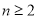 ), (10分)
), (10分)
两式相减,得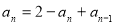 ,即
,即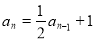 (
(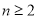 ).(11分)
).(11分)
两边减2,得 , (12分)
, (12分)
所以{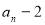 }是以-1为首项,
}是以-1为首项,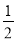 为公比的等比数列,
为公比的等比数列,
故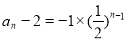 , (13分)
, (13分)
即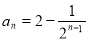 (
(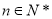 ). (14分)
). (14分)
方法二:
①当n=1时,由(1)可知猜想显然成立; (10分)
②假设当n=k时,猜想成立,即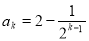 , (11分)
, (11分)
由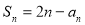 (
(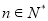 ),得
),得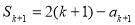 ,
,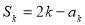
两式相减,得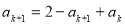 , (12分)
, (12分)
所以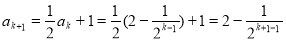 ,
,
即当n=k+1时,猜想也成立. (13分)
根据①和②,知对任意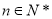 ,猜想成立.(14分)
,猜想成立.(14分)
考点:1.等比数列;2.猜想.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( ).

A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期第二次月考理科数学卷(解析版) 题型:填空题
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为
一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,
按此规律,以 表示第
表示第 幅图的蜂巢总数.则
幅图的蜂巢总数.则
 =_____,
=_____, =___________.
=___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com