
| A. | ($\frac{2}{7}$,$\frac{2}{5}$) | B. | ($\frac{2}{5}$,+∞) | C. | (-∞,$\frac{2}{7}$) | D. | (-$\frac{2}{11}$,0) |
分析 由方程有两实根可知方程为二次方程,根据题意可知方程所对应的二次函数的图象与x轴交点分别在1的两侧,由此得到1所对应的函数值得符号,即可求解.
解答 解:
由题意可知:a≠0,
设f(x)=ax2+(a+2)x+9a,
因为方程两根一个比1大,一个比1小,
∴函数图象与x轴交点分别在1两侧,
∴$\left\{\begin{array}{l}{a>0}\\{f(1)=11a+2<0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{f(1)=11a+2>0}\end{array}\right.$,
解得:$-\frac{2}{11}<a<0$.
故选:D.
点评 本题考查二次方程根的分布.正确利用方程得根与函数零点之间的关系,转化为函数图象与x轴交点的位置问题是解题关键.考查了数形结合的思想方法,属于中档题.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<0} | B. | {x|0<x≤1} | C. | {x|0≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{4}$$\overrightarrow{OC}$ | B. | $\frac{1}{4}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | C. | $\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | D. | $\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
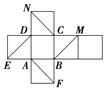 如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )
如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 相交 | C. | AC在平面DEF内 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
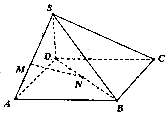 在四棱锥S-ABCD中,底面ABCD是平行四边形,M、N分别是SA,BD上的点.
在四棱锥S-ABCD中,底面ABCD是平行四边形,M、N分别是SA,BD上的点.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com