
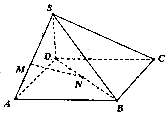
 在四棱锥S-ABCD中,底面ABCD是平行四边形,M、N分别是SA,BD上的点.
在四棱锥S-ABCD中,底面ABCD是平行四边形,M、N分别是SA,BD上的点.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 在①和②中,过M作MH∥SD,交AD于H,连结HN,由条件能推导出平面MNH∥平面SDC,从而得到MN∥面SCD;在③中,由面SDA⊥面ABCD,且面SDB⊥面ABCD,平面SDA∩平面SDB=SD,得到SD⊥面ABCD.
解答 解:在①中,过M作MH∥SD,交AD于H,连结HN,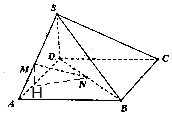
∵在四棱锥S-ABCD中,底面ABCD是平行四边形,
M、N分别是SA,BD上的点,$\frac{SM}{MA}$=$\frac{DN}{NB}$,
∴NH∥CD,
∵MH∩MN=M,SD∩DC=D,MH,MN?平面MNH,
SD,CD?平面SDC,
∴平面MNH∥平面SDC,
∵MN?平面MNH,∴MN∥面SCD,故①正确;
在②中,过M作MH∥SD,交AD于H,连结HN,
∵在四棱锥S-ABCD中,底面ABCD是平行四边形,
M、N分别是SA,BD上的点,$\frac{SM}{MA}$=$\frac{NB}{DN}$,
∴∴NH∥CD,
∵MH∩MN=M,SD∩DC=D,MH,MN?平面MNH,SD,CD?平面SDC,
∴平面MNH∥平面SDC,
∵MN?平面MNH,∴MN∥面SCD,故②正确;
在③中,∵面SDA⊥面ABCD,且面SDB⊥面ABCD,
平面SDA∩平面SDB=SD,∴SD⊥面ABCD,故③正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{7}$,$\frac{2}{5}$) | B. | ($\frac{2}{5}$,+∞) | C. | (-∞,$\frac{2}{7}$) | D. | (-$\frac{2}{11}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f($\sqrt{ab}$)<f($\frac{a+b}{2}$) | B. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(b) | C. | f($\sqrt{ab}$)<f($\frac{a+b}{2}$)<f(a) | D. | f(a)>f($\sqrt{ab}$)>f($\frac{a+b}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若函数y=f(x)为奇函数,则f(0)=0 | |
| B. | 函数f(x)=(x-1)-1在(-∞,1)∪(1,+∞)上单调减函数 | |
| C. | 要得到y=f(2x-2)的图象,只需要将y=f(2x)的图象向右平移1个单位 | |
| D. | 若函数y=f(2x+1)的定义域为[2,3],则函数y=f(x)的定义域为[0.5,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{4}$] | B. | [-$\frac{1}{4}$,0] | C. | (-∞,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com