
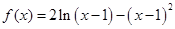 .
.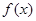 的单调递增区间;
的单调递增区间;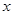 的方程
的方程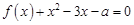 在区间
在区间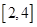 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数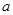 的取值范围.
的取值范围. 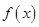 的单调递增区间为
的单调递增区间为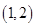 .(2)
.(2)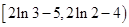 .
. 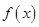 的定义域为
的定义域为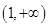 ,………………………………………………1分
,………………………………………………1分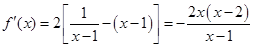 , ………………………………………2分
, ………………………………………2分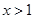 ,则使
,则使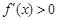 的
的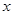 的取值范围为
的取值范围为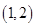 ,
,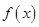 的单调递增区间为
的单调递增区间为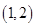 . ……………………………………………4分
. ……………………………………………4分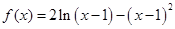 ,
,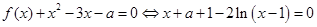 . …………………………6分
. …………………………6分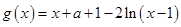 ,
, 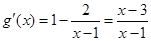 ,且
,且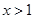 ,
,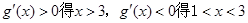 .
.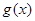 在区间
在区间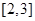 内单调递减,在区间
内单调递减,在区间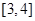 内单调递增, ……………………8分
内单调递增, ……………………8分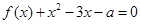 在区间
在区间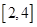 内恰有两个相异实根
内恰有两个相异实根 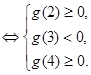 ……10分
……10分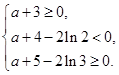 解得:
解得: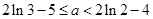 .
.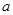 的取值范围是
的取值范围是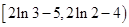 . ………………………………12分
. ………………………………12分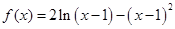 ,
,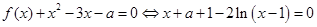 . …………………………6分
. …………………………6分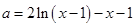 ,
,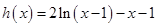 , ∵
, ∵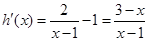 ,且
,且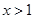 ,
,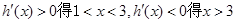 .
.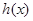 在区间
在区间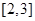 内单调递增,在区间
内单调递增,在区间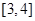 内单调递减.……………………8分
内单调递减.……………………8分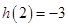 ,
,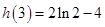 ,
,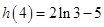 ,
,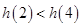 ,
,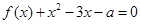 在区间
在区间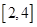 内恰有两个相异实根
内恰有两个相异实根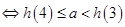 .
.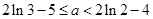 .
.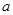 的取值范围是
的取值范围是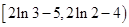 . ……………………………12分
. ……………………………12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
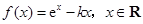
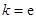 ,试确定函数
,试确定函数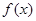 的单调区间;
的单调区间;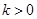 ,且对于任意
,且对于任意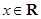 ,
,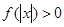 恒成立,试确定实数
恒成立,试确定实数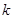 的取值范围;
的取值范围;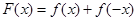 ,求证:
,求证: .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
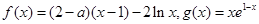 ,(
,(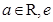 为自然对数的底数)。
为自然对数的底数)。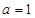 时,求函数
时,求函数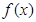 在区间
在区间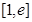 上的最大值和最小值;
上的最大值和最小值; 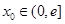 ,在
,在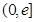 上总存在两个不同的
上总存在两个不同的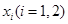 ,使得
,使得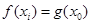 成立,求
成立,求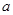 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
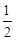 x2+ex-xex.(1)求f(x)的单调区间;
x2+ex-xex.(1)求f(x)的单调区间;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =
=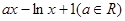 ,
,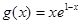 .
.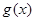 在区间
在区间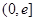 上的值域;
上的值域;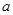 ,对任意给定的
,对任意给定的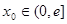 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的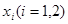 ,使得
,使得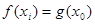 成立.若存在,求出
成立.若存在,求出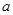 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.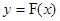 图象上任意不同的两点
图象上任意不同的两点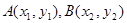 ,如果对于函数
,如果对于函数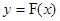 图象上的点
图象上的点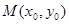 (其中
(其中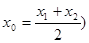 总能使得
总能使得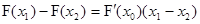 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数 是不是具备性质“
是不是具备性质“ ”,并说明理由.
”,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
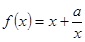 的定义域为(0,
的定义域为(0,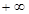 ),且
),且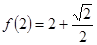 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线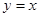 和
和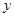 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N.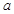 的值;
的值;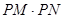 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;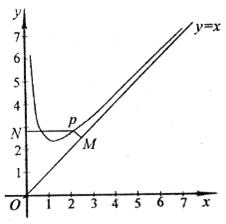
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com