Question

（本小题满分12分）
已知集合A＝{a²，a＋1，－3}，B＝{a－3，a²＋1,2a－1}，若A∩B＝{－3}，
（Ⅰ）求实数a的值．
（Ⅱ）设，求不等式的解集。

Answer 1

（1）a＝－1.（2）(－3,1)∪(3，＋∞)

解析试题分析：（Ⅰ）　∵A∩B＝{－3}，∴－3∈B，
∴当a－3＝－3，即a＝0时，A∩B＝{－3,1}，与题设条件A∩B＝{－3}矛盾，舍去；
当2a－1＝－3，即a＝－1时，A＝{1,0，－3}，B＝{－4,2，－3}，
满足A∩B＝{－3}，综上可知a＝－1.………………………………6分
（Ⅱ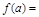）∵f(1)＝3，∴当x≥0时，由f(x)＞f(1)得x²－4x＋6>3，
∴x＞3或x＜1.又x≥0，∴x∈[0,1)∪(3，＋∞)．
当x＜0时，由f(x)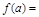＞3得x＋6＞3∴x＞－3，
∴x∈(－3,0)．
∴所求不等式的解集为： (－3,1)∪(3，＋∞) ……………………12分
考点：本试题考查了集合的交集，一元二次不等式的求解。
点评：解决该试题的关键是要利用集合运算的特性：互异性来确定参数a的值。从-3是公共的元素入手来分析，而对于分段函数的不等式的求解，需要对x进行分类讨论得到。属于中档题。