Question

4．给出定义：若m-$\frac{1}{2}＜$x≤m+$\frac{1}{2}$（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m．在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题．
①函数y=f（x）的定义域是R，值域是[0，$\frac{1}{2}$]
②函数y=f（x）的图象关于x=$\frac{k}{2}$（k∈Z）对称；
③函数y=f（x）的图象关于点（$\frac{k}{2}$，0）（k∈Z）对称；
④函数y=f（x）是周期函数，最小正周期是1；
⑤函数y=f（x）在[-$\frac{1}{2}$，$\frac{1}{2}$]上是增函数；
其中真命题是（填上所有真命题的序号）①②④．

Answer 1

分析 根据题意，先对函数化简，然后作出函数的图象，根据函数的图象可判断各个选项是否正确

解答 解：∵函数f（x）=|x-{x}|的图象如下图所示：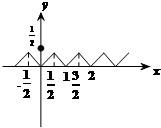

由图可知：
①函数y=f（x）的定义域是R，值域是[0，$\frac{1}{2}$]，故正确；
②函数y=f（x）的图象关于x=$\frac{k}{2}$（k∈Z）对称，故正确；
③函数y=f（x）的图象关于点（$\frac{k}{2}$+$\frac{1}{4}$，0）（k∈Z）对称，故错误；
④函数y=f（x）是周期函数，最小正周期是1，故正确；
⑤函数y=f（x）在[-$\frac{1}{2}$，0]上是减函数，在[0，$\frac{1}{2}$]上是增函数，故错误；
故答案为：①②④

点评 本题考查函数的性质和应用，解题时要认真审题，仔细解答，注意函数的定义域、值域、对称性和周期性的求法．