
分析 首先写出第二象限的角的集合,然后分别得到-α,π+α,π-α,$\frac{π}{2}$+α的范围得答案.
解答 解:∵α是第二象限角,
∴$\frac{π}{2}+2kπ<α<π+2kπ,k∈Z$,
则$-π-2kπ<-α<-\frac{π}{2}-2kπ,k∈Z$,-α是第三象限的角;
$\frac{3}{2}π+2kπ<π+α<2π+2kπ,k∈Z$,π+α是第四象限角;
$-2kπ<π-α<\frac{π}{2}-2kπ,k∈Z$,π-α是第一象限角;
$π+2kπ<\frac{π}{2}+α<\frac{3π}{2}+2kπ,k∈Z$,$\frac{π}{2}$+α是第三象限角.
点评 本题考查了象限角和轴线角,是基础的会考题型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:解答题
已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(1)当 时,求过点
时,求过点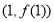 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数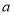 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18$\sqrt{3}$ | B. | 20$\sqrt{3}$ | C. | 22$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,-4) | B. | (10,-4) | C. | (10,4) | D. | (8,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com