Question

8．函数y=x²一点P（非原点），在P处引切线交x轴，y轴于Q，R，求$\frac{|PQ|}{|PR|}$．

Answer 1

分析 如图所示，设切点P$（{x}_{0}，{x}_{0}^{2}）$，利用导数的几何可得切线的斜率，得到切线方程，即可得出点Q，R的坐标．即可得出．

解答 解：如图所示，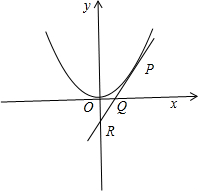
设切点P$（{x}_{0}，{x}_{0}^{2}）$，
∵y′=2x，
∴切线的斜率为：k=2x₀，
∴切线方程为：$y-{x}_{0}^{2}=2{x}_{0}（x-{x}_{0}）$，
令y=0，可得x=$\frac{{x}_{0}}{2}$，∴Q$（\frac{{x}_{0}}{2}，0）$；
令x=0，可得$y=-{x}_{0}^{2}$，∴R$（0，-{x}_{0}^{2}）$．
可知：Q点为线段PR的中点，
∴$\frac{|PQ|}{|PR|}$=$\frac{1}{2}$．

点评 本题考查了导数的几何意义、抛物线的切线方程、中点坐标公式，考查了推理能力与计算能力，属于中档题．