
由不等式组 围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
A.P′(t)>0 B.P′(t)<0 C.P′(t)=0 D.P′(t)符号不确定
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:填空题
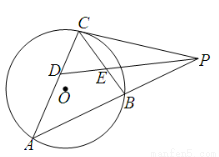
如图,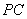 是圆
是圆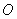 的切线,切点为点
的切线,切点为点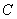 ,直线
,直线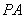 与圆
与圆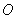 交于
交于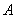 、
、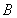 两点,
两点,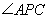 的角平分线交弦
的角平分线交弦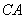 、
、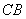 于
于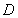 、
、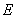 两点,已知
两点,已知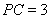 ,
,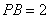 ,则
,则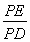 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:解答题
已知函数f(x)=tan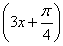 .
.
(1)求f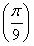 的值;
的值;
(2)设α∈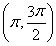 ,若f
,若f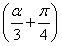 =2,求cos
=2,求cos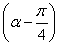 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:解答题
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
|
|
|
|
|
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
(1)计算x,y的值;
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
参考数据与公式:由列联表中数据计算K2=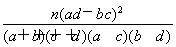 . ?
. ?
临界值表
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:填空题
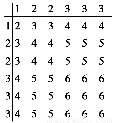
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
A.32 B.0.2 C.40 D.0.25
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
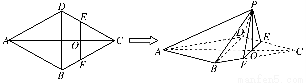
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷2练习卷(解析版) 题型:解答题
已知函数f(x)=2sin2 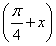 -
-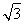 cos 2x-1(x∈R).
cos 2x-1(x∈R).
(1)若函数h(x)=f(x+t)的图象关于点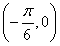 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;
(2)设p:x∈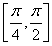 ,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com