
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为 ![]() ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为 ![]() .
.
(1)求圆C的普通方程和直线l的直角坐标方程;
(2)点P是圆C上任一点,求△PAB面积的最小值.
【答案】
(1)解:由 ![]() ,化简得:
,化简得: ![]() ,
,
消去参数t,得(x+5)2+(y﹣3)2=2,
∴圆C的普通方程为(x+5)2+(y﹣3)2=2.
由ρcos(θ+ ![]() )=﹣
)=﹣ ![]() ,化简得
,化简得 ![]() ρcosθ﹣
ρcosθ﹣ ![]() ρsinθ=﹣
ρsinθ=﹣ ![]() ,
,
即ρcosθ﹣ρsinθ=﹣2,即x﹣y+2=0,
则直线l的直角坐标方程为x﹣y+2=0
(2)解:将A(2, ![]() ),B(2,π)化为直角坐标为A(0,2),B(﹣2,0),
),B(2,π)化为直角坐标为A(0,2),B(﹣2,0),
∴|AB|= ![]() =2
=2 ![]() ,
,
设P点的坐标为(﹣5+ ![]() cost,3+
cost,3+ ![]() sint),
sint),
∴P点到直线l的距离为d= ![]() =
= ![]() ,
,
∴dmin= ![]() =2
=2 ![]() ,
,
则△PAB面积的最小值是S= ![]() ×2
×2 ![]() ×2
×2 ![]() =4.
=4.
【解析】(1)由圆C的参数方程消去t得到圆C的普通方程,由直线l的极坐标方程,利用两角和与差的余弦函数公式化简,根据x=ρcosθ,y=ρsinθ转化为直角坐标方程即可;(2)将A与B的极坐标化为直角坐标,并求出|AB|的长,根据P在圆C上,设出P坐标,利用点到直线的距离公式表示出P到直线l的距离,利用余弦函数的值域确定出最小值,即可确定出三角形PAB面积的最小值.
【考点精析】根据题目的已知条件,利用圆的参数方程的相关知识可以得到问题的答案,需要掌握圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B均为锐角,则cosA>sinB是△ABC为钝角三角形的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,则其长轴长为__________;若
,则其长轴长为__________;若![]() 为
为![]() 的右焦点,
的右焦点, ![]() 为
为![]() 的上顶点,
的上顶点, ![]() 为
为![]() 上位于第一象限内的动点,则四边形
上位于第一象限内的动点,则四边形![]() 的面积的最大值为__________.
的面积的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的一年收益与投资额成正比,其关系如图(1);投资股票等风险型产品的一年收益与投资额的算术平方根成正比,其关系如图(2).(注:收益与投资额单位:万元)
(1)分别写出两种产品的一年收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使一年的投资获得最大收益,其最大收益是多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x2)+ax.(a≤0)
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() (n∈N* , e为自然对数的底数).
(n∈N* , e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
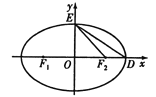
【题目】如图![]() 为椭圆C:
为椭圆C:![]()
![]() 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率![]() ,
,![]() 的面积为
的面积为![]() .若点
.若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线![]() 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点![]() 的直线
的直线![]() ,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆x2+ ![]() =1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距为2
=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距为2 ![]() ,点P是Γ上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为k,O为坐标原点.
,点P是Γ上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为k,O为坐标原点. 
(1)求双曲线Γ的方程;
(2)求点M的纵坐标yM的取值范围;
(3)是否存在定直线l,使得直线BP与直线OM关于直线l对称?若存在,求直线l方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则函数表达式为;若将该函数向左平移1个单位,再保持纵坐标不变,横坐标缩短为原来的 ![]() 倍得到函数g(x)= .
倍得到函数g(x)= . 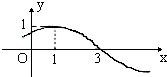
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com