
【题目】第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办,设置“三馆两园一带一谷一线”八大功能板块.现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作,若每个“馆”与“园”都至少安排一人,则不同的安排方法种数为( )
A.C ![]() A
A ![]()
B.5C ![]() A
A ![]()
C.5A ![]()
D.C ![]() A
A ![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(1,﹣2),直线l: ![]() (m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(1)求直线l和曲线C的普通方程;
(2)求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体A﹣BCD中,AB=CD=10,AC=BD=2 ![]() ,AD=BC=2
,AD=BC=2 ![]() ,则四面体A﹣BCD外接球的表面积为( )
,则四面体A﹣BCD外接球的表面积为( )
A.50π
B.100π
C.200π
D.300π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD, ![]() ,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.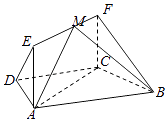
(1)求证:EF⊥平面BCF;
(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxsin( ![]() ﹣x).
﹣x).
(Ⅰ)求f( ![]() )及f(x)的最小正周期T的值;
)及f(x)的最小正周期T的值;
(Ⅱ)求f(x)在区间[﹣ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )的图象过点
)的图象过点 ![]() ,且在(
,且在( ![]() ,
, ![]() )上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当
)上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当 ![]() ,且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
,且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
A.﹣ ![]()
B.﹣1
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在x1处取得极大值,在x2处取得极小值,满足x1∈(﹣1,0),x2∈(0,1),则
在x1处取得极大值,在x2处取得极小值,满足x1∈(﹣1,0),x2∈(0,1),则 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.(0,1)
C.![]()
D.[1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() 、
、 ![]() 是两个相交平面,则在下列命题中,真命题的序号为( )
是两个相交平面,则在下列命题中,真命题的序号为( )
①若直线 ![]() ,则在平面
,则在平面 ![]() 内一定不存在与直线
内一定不存在与直线 ![]() 平行的直线.
平行的直线.
②若直线 ![]() ,则在平面
,则在平面 ![]() 内一定存在无数条直线与直线
内一定存在无数条直线与直线 ![]() 垂直.
垂直.
③若直线 ![]() ,则在平面
,则在平面 ![]() 内不一定存在与直线
内不一定存在与直线 ![]() 垂直的直线.
垂直的直线.
④若直线 ![]() ,则在平面
,则在平面 ![]() 内一定存在与直线
内一定存在与直线 ![]() 垂直的直线.
垂直的直线.
A.①③
B.②③
C.②④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com