[题目]已知函数f(x)=2sinxsin( ﹣x)．(Ⅰ)求f( )及f(x)的最小正周期T的值,在区间[﹣ . ]上的最大值和最小值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f（x）=2sinxsin（ ﹣x）．
（Ⅰ）求f（）及f（x）的最小正周期T的值；
（Ⅱ）求f（x）在区间[﹣ ， ]上的最大值和最小值．

【答案】解：（Ⅰ）函数f（x）=2sinxsin（ ﹣x）=2sinx（ cosx﹣ sinx）

= sin2x﹣ sin2x= sin2x﹣ = sin2x+ cos2x﹣ =sin（2x+ ）﹣ ，

∴f（）=sinπ﹣ =﹣ ，∴T= =π．

（Ⅱ）在区间[﹣ ， ]上，2x+ ∈[0， ]，

∴当2x+ = 时，函数f（x）取得最大值为1﹣ ，

当2x+ =0时，函数f（x）取得最小值为0﹣ =﹣ ．

【解析】（1）由两角和差公式可得f（x）=sin（2x+ ）﹣ ，得结果。
（2）整体思想可得当2x+ π 3 = π 2 时，函数f（x）取得最大值为1﹣ ，当2x+ =0时，函数f（x）取得最小值为0﹣ =﹣ ．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为矩形，M是AD上一点．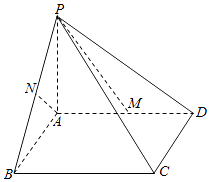

（1）求证：AB⊥PM；
（2）若N是PB的中点，且AN∥平面PCM，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= ．
（1）证明：k∈R，直线y=g（x）都不是曲线y=f（x）的切线；
（2）若x∈[e，e2]，使得f（x）≤g（x）+ 成立，求实数k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】数列{an}是公差为d（d≠0）的等差数列，Sn为其前n项和，a1 ， a2 ， a5成等比数列．
（Ⅰ）证明S1 ， S3 ， S9成等比数列；
（Ⅱ）设a1=1，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办，设置“三馆两园一带一谷一线”八大功能板块．现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作，若每个“馆”与“园”都至少安排一人，则不同的安排方法种数为（　　）
A.C A
B.5C A
C.5A
D.C A

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设集合U={1，2，…，100}，TU．对数列{an}（n∈N*），规定：
①若T=，则ST=0；
②若T={n1 ， n2 ， …，nk}，则ST=a +a +…+a ．
例如：当an=2n，T={1，3，5}时，ST=a1+a3+a5=2+6+10=18．
已知等比数列{an}（n∈N*），a1=1，且当T={2，3}时，ST=12，求数列{an}的通项公式．