
【题目】下列计算曲线y=cosx(0≤x≤ ![]() )与坐标轴围成的面积:
)与坐标轴围成的面积:
(1)![]() cosxdx,(2)3
cosxdx,(2)3 ![]() cosxdx,(3)
cosxdx,(3) ![]() |cosx|dx,(4)面积为3.
|cosx|dx,(4)面积为3.
用的方法或结果正确的是 .
【答案】
(1)(2)、(3)、(4)
【解析】解:∵当0≤x≤ ![]() ,时,cosx≥0,当
,时,cosx≥0,当 ![]() ≤x≤
≤x≤ ![]() 时,cosx≤0,
时,cosx≤0,
∴曲线y=cosx(0≤x≤ ![]() )与坐标轴围成的面积S=
)与坐标轴围成的面积S= ![]() cosxdx﹣
cosxdx﹣ ![]() cosxdx,
cosxdx,
(1) ![]() cosxdx,错误,
cosxdx,错误,
(2)函数在0≤x≤ ![]() ,
, ![]() ≤x≤π,π≤x≤
≤x≤π,π≤x≤ ![]() 三段的面积相同,
三段的面积相同,
则S=3 ![]() cosxdx,正确
cosxdx,正确
(3) ![]() |cosx|dx,正确
|cosx|dx,正确
(4)面积为S=3 ![]() cosxdx=3sinx|
cosxdx=3sinx| ![]() =3(sin
=3(sin ![]() ﹣sin0)=3.
﹣sin0)=3.
正确,
所以答案是:(2)、(3)、(4);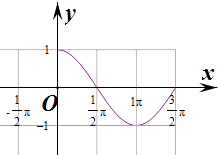
【考点精析】掌握定积分的概念是解答本题的根本,需要知道定积分的值是一个常数,可正、可负、可为零;用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由
是由![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() .现将
.现将![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]() 的大小为90°,得到图形如图(2)所示,连接
的大小为90°,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(Ⅰ)证明: ![]() ;
;
(Ⅱ)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且 PB=PC= ![]() .
.
(Ⅰ)求证:AB⊥CP;
(Ⅱ)求点B到平面PAD的距离;
(Ⅲ)设面PAD与面PBC的交线为l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是 ![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣x2﹣
x3﹣x2﹣ ![]() x,则f(﹣a2)与f(﹣1)的大小关系为( )
x,则f(﹣a2)与f(﹣1)的大小关系为( )
A.f(﹣a2)≤f(﹣1)
B.f(﹣a2)<f(﹣1)
C.f(﹣a2)≥f(﹣1)
D.f(﹣a2)与f(﹣1)的大小关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一点在直线上从时刻t=0(s)开始以速度v(t)=t2﹣4t+3(m/s)运动,求:
(1)在t=4s时的位置;
(2)在t=4s的运动路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com