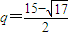【答案】
分析:(1)根据解析式判断f(x)在区间[-1,1]上递减,由函数零点的几何意义知f(-1)•f(1)≤0,再代入方程后求不等式得解集,即是p的范围;
(2)先假设存在常数q(q≥0)满足题意,根据对称轴和区间[q,10]的关系进行分类,再根据每种情况中的二次函数图象求出函数的值域,利用区间长度求出q的值,注意验证是否在确定的范围内.
解答:解:(1)∵二次函数f(x)=x
2-16x+p+3的对称轴是x=8,
∴函数f(x)在区间[-1,1]上单调递减,
则函数f(x)在区间[-1,1]上存在零点须满足f(-1)•f(1)≤0.
即(1+16+p+3)(1-16+p+3)≤0,解得-20≤p≤12.
(2)假设存在常数q(q≥0)满足题意,分三种情况求解:
①当
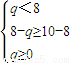
时,即0≤q≤6时,
当x=8时,取到最小值f(8);当x=q时,取到最大值f(q),
∴f(x)的值域为:[f(8),f(q)],即[p-61,q
2-16q+p+3].
∴区间长度为q
2-16q+p+3-(p-61)=q
2-16q+64=12-q.
∴q
2-15q+52=0,∴
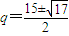
,经检验
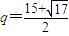
不合题意,舍去,故
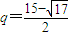
.
②当
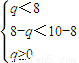
时,即6≤q<8时,
当x=8时,取到最小值f(8);当x=10时,取到最大值f(10),
∴f(x)的值域为:[f(8),f(10)],即[p-61,p-57]
∴区间长度为p-57-(p-61)=4=12-q,∴q=8.经检验q=8不合题意,舍去.
③当q≥8时,函数f(x)在[q,10]上单调递增,
∴f(x)的值域为:[f(q),f(10)],即[q
2-16q+p+3,p-57].
∴区间长度为p-57-(q
2-16q+p+3)=-q
2-16q-60=12-q,
∴q
2-17q+72=0,∴q=8或q=9.经检验q=8或q=9满足题意.
综上知,存在常数q=8或q=9,
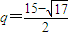
当x∈[q,10]时,f(x)的值域为区间D,且D的长度为12-q.
点评:本题考查了函数零点的几何意义和在给定区间上求二次函数的值域,特别是区间含有参数时,要讨论对称轴和区间的位置关系并由此进行分类,是综合性强和计算量大的题.

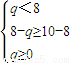 时,即0≤q≤6时,
时,即0≤q≤6时,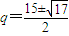 ,经检验
,经检验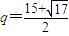 不合题意,舍去,故
不合题意,舍去,故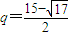 .
.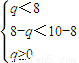 时,即6≤q<8时,
时,即6≤q<8时,