
| A. | ($\frac{1-\sqrt{5}}{2}$,$\frac{1+\sqrt{5}}{2}$) | B. | (-1,$\frac{1+\sqrt{5}}{2}$) | C. | ($\frac{1-\sqrt{5}}{2}$,0) | D. | ($\frac{1-\sqrt{5}}{2}$,-$\frac{1}{2}$] |
分析 考虑a=0,a>0不成立,当a<0时,画出f(x)的图象和f(x+a)的大致图象,考虑x=-$\frac{1}{2}$时两函数值相等,解方程可得a的值,随着y=f(x+a)的图象左移至f(x)的过程中,均有f(x)的图象恒在f(x+a)的图象上,即可得到a的范围.
解答 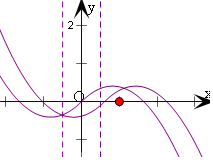 解:a=0时,显然不符题意;
解:a=0时,显然不符题意;
当x∈[-$\frac{1}{2}$,$\frac{1}{2}$]时,恒有f(x+a)<f(x),
即为f(x)的图象恒在f(x+a)的图象之上,
则a<0,即f(x)的图象右移.
故A,B错;
画出函数f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x,x≥0}\\{-a{x}^{2}+x,x<0}\end{array}\right.$(a<0)的图象,
当x=-$\frac{1}{2}$时,f(-$\frac{1}{2}$)=-a•$\frac{1}{4}$-$\frac{1}{2}$;
而f(x+a)=$\left\{\begin{array}{l}{a(x+a)^{2}+x+a,x≥-a}\\{-a(x+a)^{2}+x+a,x<-a}\end{array}\right.$,
则x=-$\frac{1}{2}$时,由-a(-$\frac{1}{2}$+a)2+a-$\frac{1}{2}$=-a•$\frac{1}{4}$-$\frac{1}{2}$,
解得a=$\frac{1-\sqrt{5}}{2}$($\frac{1+\sqrt{5}}{2}$舍去),
随着f(x+a)的图象左移至f(x)的过程中,均有f(x)的图象恒在f(x+a)的图象上,
则a的范围是($\frac{1-\sqrt{5}}{2}$,0),
故选:C.
点评 本题考查不等式恒成立问题解法,注意运用转化思想,化为图象之间的关系,由图象平移结合数形结合思想方法,考查运算能力,属于难题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
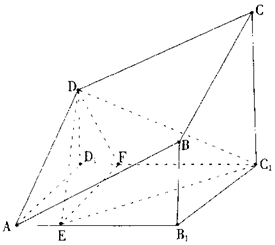 如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
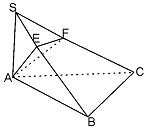 如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com