
(1)求这批食品不能出厂的概率(保留三位有效数字);
(2)求直至五项指标全部检验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
分析:设五项指标中抽检时不合格的指标数为X,则X—B(5,0.2).
解:(1)五项指标抽检,有2项、3项、4项、5项指标不合格,则这批食品均不能出厂,其对立事件是五项指标抽检,全合格或有一项指标不合格,所以这批食品不能出厂的概率为
P(X≥2)=1-P(X=0)-P(X=1)=1-[C![]() (1-0.2)5+C
(1-0.2)5+C![]() 0.21(1-0.2)4]=0.262 72≈0.263.
0.21(1-0.2)4]=0.262 72≈0.263.
(2)直至五项指标全部检验完毕,才能确定该批产品是否出厂,即为:前4项指标检验中恰有一项指标不合格,故所求的概率为
p2=C![]() 0.21(1-0.2)3=0.409 6≈0.410.
0.21(1-0.2)3=0.409 6≈0.410.
绿色通道:(1)中利用了对立事件的概率来简化计算;(2)中的随机变量虽然也服从二项分布,但参数发生了变化,由(1)中的n=5变为n=4.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
有一批食品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是![]() .
.
(1)求这批产品不能出厂的概率(保留三位有效数字);
(2)求直至五项指标全部验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).查看答案和解析>>
科目:高中数学 来源: 题型:
有一批食品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是0.2.
⑴求这批产品不能出厂的概率(保留三位有效数字);
⑵求直至五项指标全部验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-32.5离散型随机变量均值与方差练习卷(解析版) 题型:解答题
有一批食品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是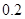 .
.
(1)求这批产品不能出厂的概率(保留三位有效数字);
(2)求直至五项指标全部验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com