练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．四个不同的小球放入编号为1，2，3，4的四个盒子中．
    （1）若每个盒子放一球，则有多少种不同的放法？
    （2）恰有一个空盒的放法共有多少种？

    分析 （1）每个盒子均有一球，也就是4个元素的排列；
    （2）由题意知需要先选两个元素作为一组再排列，恰有一个盒子中有2个小球，从4个小球中选两个作为一个元素，同另外两个元素在三个位置全排列，根据分步计数原理得到结果．

    解答 解：（1）每个盒子均有一球，也就是4个元素的排列，故有A44=24种不同的放法；
    （2）四个不同的小球放入编号为1，2，3，4的四个盒子中，恰有一个空盒，说明恰有一个盒子中有2个小球，
    从4个小球中选两个作为一个元素，同另外两个元素在三个位置全排列，故共有C42A43=144种不同的放法．

    点评 本题考查分步计数原理，是一中档题，解题的过程中注意这种有条件的排列要分步走，先选元素再排列．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=（x2+ax）ex的两个极值为x1，x1，且x1+x1=-2-$\sqrt{5}$．
    （1）求x1，x1的值；
    （2）若f（x）在（c-1，c）（其中c＜-1）上是单调函数，求c的取值范围；
    （3）当m≤-e，求证：[f（x）+2ex]•[（x-2）ex-m+1]＞$\frac{3}{4}$ex．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．某中学有甲乙两个文科班进行数学考试，按照大于或等于120分为优秀，120分以下为非优秀统计成绩后，得到如下列联表：
    优秀非优秀合计
    甲20525
    乙101525
    合计302050
    （1）用分层抽样的方法在优秀的学生中抽6人，其中甲班抽多少人？
    （2）计算出统计量k2，能否有95%的把握认为“成绩与班级有关”？
    下面的临界值表代参考：
    P（k2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．函数y=x-ex的增区间为（　　）
    A．（1，+∞）B．（-∞，0）C．（0，+∞）D．（-∞，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知f′（x）为y=f（x）的导函数，且f′（x0）=a，则$\lim_{△x→0}\frac{{f（{x_0}-△x）-f（{x_0}）}}{△x}$=（　　）
    A．aB．-aC．±aD．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．方程x2-mnx+m+n=0有整数根，且m．n为自然数，则m、n的有几对，试求出来．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在四面体S-ABC中，SA⊥平面ABC，△ABC是边长为3的正三角形，SA=2，则该四面体的外接球的表面积为（　　）
    A．8πB．12πC．16πD．32π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

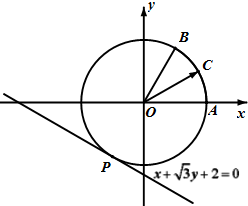    16．如图，圆O与直线x+$\sqrt{3}$y+2=0相切于点P，与x正半轴交于点A，与直线y=$\sqrt{3}$x在第一象限的交点为B．点C为圆O上任一点，且满足$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，以x，y为坐标的动点D（x，y）的轨迹记为曲线Γ．
    （1）求圆O的方程及曲线Γ的方程；
    （2）若两条直线l1：y=kx和l2：y=-$\frac{1}{k}$x分别交曲线Γ于点E、F和M、N，求四边形EMFN面积的最大值，并求此时的k的值．
    （3）根据曲线Γ的方程，研究曲线Γ的对称性，并证明曲线Γ为椭圆．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．用“五点法”画函数y=-2+sinx（x∈[0，2π]）的简图．

    查看答案和解析>>

    同步练习册答案