
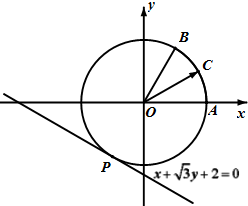
 如图,圆O与直线x+$\sqrt{3}$y+2=0相切于点P,与x正半轴交于点A,与直线y=$\sqrt{3}$x在第一象限的交点为B.点C为圆O上任一点,且满足$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,以x,y为坐标的动点D(x,y)的轨迹记为曲线Γ.
如图,圆O与直线x+$\sqrt{3}$y+2=0相切于点P,与x正半轴交于点A,与直线y=$\sqrt{3}$x在第一象限的交点为B.点C为圆O上任一点,且满足$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,以x,y为坐标的动点D(x,y)的轨迹记为曲线Γ.分析 (1)圆O与直线x+$\sqrt{3}$y+2=0相切于点,利用点到直线的距离,即可求出半径,解得圆的方程.根据$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$和坐标关系带入圆的方程,即可得到曲线Γ的方程;垂直
(2)两条直线l1:y=kx和l2:y=-$\frac{1}{k}$x分别交曲线Γ,解出坐标,由题意l1与l2垂直,利用两点之间的距离求出EF,MN长度,即可得到四边形的面积,利用基本不等式即可得到答案.
(3)根据(1)中得到的方程,首先考虑奇偶性和x轴,y=x轴的对称,在考虑非常见对称.利用椭圆的定义证明即可.
解答 解:由题意:圆O与直线x+$\sqrt{3}$y+2=0相切于点,利用点到直线的距离,即可求出半径,
r=$\frac{2}{\sqrt{1+(\sqrt{3})^{2}}}=1$
∴圆的方程为:x2+y2=1
圆与x轴的交点A(1,0),与直线y=$\sqrt{3}$x在第一象限的交点B为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
由$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,可得:$\overrightarrow{OC}=(x+\frac{1}{2}y,\;\frac{{\sqrt{3}}}{2}y)$,将$C(x+\frac{1}{2}y,\;\frac{{\sqrt{3}}}{2}y)$代入x2+y2=1
得到:x2+y2+xy=1,($x,y∈[-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3}]$)即为曲线Γ的方程;
(2)∵两条直线l1:y=kx和l2:y=-$\frac{1}{k}$x分别交曲线Γ于点E、F和M、N.
∴联立:$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{y}^{2}+xy=1}\end{array}\right.$⇒解得:点E($\frac{1}{\sqrt{{k}^{2}+k+1}}$,$\frac{k}{\sqrt{{k}^{2}+k+1}}$),点F(-$\frac{1}{\sqrt{{k}^{2}+k+1}}$,-$\frac{k}{\sqrt{{k}^{2}+k+1}}$)
那么:|EF|=$2\sqrt{\frac{{k}^{2}+1}{{k}^{2}+k+1}}$
同理:
联立$\left\{\begin{array}{l}{k=\frac{1}{-k}x}\\{{x}^{2}+{y}^{2}+xy=1}\end{array}\right.$⇒解得:点M($\frac{1}{\sqrt{\frac{1}{{k}^{2}}-\frac{1}{k}+1}}$,$\frac{\frac{1}{k}}{\sqrt{\frac{1}{{k}^{2}}-\frac{1}{k}+1}}$)点N(-$\frac{1}{\sqrt{\frac{1}{{k}^{2}}-\frac{1}{k}+1}}$,-$\frac{\frac{1}{k}}{\sqrt{\frac{1}{{k}^{2}}-\frac{1}{k}+1}}$)
那么:|MN|=$2\sqrt{\frac{{k}^{2}+1}{{k}^{2}-k+1}}$
由题意可知:l1⊥l2,所以四边形EMFN面积的为S=$\frac{1}{2}$|MN|•|EF|=2$\sqrt{\frac{{k}^{2}+1}{{k}^{2}+k+1}}$×$\sqrt{\frac{{k}^{2}+1}{{k}^{2}-k+1}}$=$\sqrt{1-\frac{1}{{k}^{2}+\frac{1}{{k}^{2}}+2}}$
∵$\frac{1}{{y}^{2}}+{y}^{2}≥2$.(当且仅k=±1时等号成立)
∴$\frac{S}{2}≥\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}$
⇒$S≤\frac{4\sqrt{3}}{3}$
故当k=±1时,四边形EMFN的面积最大,其最大值为:$\frac{4\sqrt{3}}{3}$.
(3)由(1)可知:曲线Γ的方程:x2+y2+xy=1,($x,y∈[-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3}]$)
关于直线y=x,也关于原点对称,同时关于直线y=-x对称
证明:
设曲线Γ上任一点的坐标为P(x0,y0),则有${{x}_{0}}^{2}+{{y}_{0}}^{2}+{x}_{0}{y}_{0}=1$
点P关于直线y=x的对称点P′(y0,x0),带入方程得:${{y}_{0}}^{2}+{{x}_{0}}^{2}+{y}_{0}{x}_{0}=1$,显然成立.
故曲线Γ的方程关于直线y=x对称.
同理:
曲线Γ的方程关于原点对称,同时关于直线y=-x对称.
证明曲线Γ为椭圆型曲线.
证明:
曲线Γ的方程:x2+y2+xy=1和直线x=y的交点坐标为B1(-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$),B2($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)
曲线Γ的方程:x2+y2+xy=1和直线x=-y的交点坐标为A1(-1,1),A2(1,-1)
|0A1|=$\sqrt{2}$,|0B1|=$\frac{\sqrt{6}}{3}$,那么$\sqrt{|0A{1|}^{2}-|0B{1|}^{2}}=\frac{2\sqrt{3}}{3}$,$\sqrt{|0A1{|}^{2}-|0B1{|}^{2}}÷\sqrt{2}=\frac{\sqrt{6}}{3}$
在y=-x上取F1(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$,),F2($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$)
设P(x,y)在曲线Γ的方程上的任意一点,则|PF1|+|PF2|=$\sqrt{(x+\frac{\sqrt{6}}{3})^{2}+(y-\frac{\sqrt{6}}{3})^{2}}+\sqrt{(x-\frac{\sqrt{6}}{3})^{2}+(y+\frac{\sqrt{6}}{3})^{2}}$=$\sqrt{{x}^{2}+{y}^{2}+\frac{4}{3}+\frac{2\sqrt{6}}{3}(x-y)}+\sqrt{{x}^{2}+{y}^{2}+\frac{4}{3}-\frac{2\sqrt{6}}{3}(x-y)}$
=$\sqrt{1-xy+\frac{4}{3}+\frac{2\sqrt{6}}{3}(x-y)}+\sqrt{1-xy+\frac{4}{3}-\frac{2\sqrt{6}}{3}(x-y)}$=$\sqrt{\frac{7}{3}-xy+\frac{2\sqrt{6}}{3}(x-y)}+\sqrt{\frac{7}{3}-xy-\frac{2\sqrt{6}}{3}(x-y)}$=$\sqrt{\frac{14}{3}-2xy+2{{\sqrt{(xy-\frac{5}{3})}}^{2}}^{\;}}$=$\sqrt{\frac{14}{3}-2xy+2(xy-\frac{5}{3})}$
因为xy≤$\frac{4}{3}$,
∴$\sqrt{\frac{14}{3}-2xy+2(xy-\frac{5}{3})}$=2$\sqrt{2}$=|A1A2|
即曲线Γ的方程上的任意一点P到两个定点F1(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$,),F2($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$)的距离之和为定值2$\sqrt{2}$.
可以反过来证明:
若点P到两个定点F1(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$,),F2($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$)的距离之和为定值2$\sqrt{2}$,可以求得P的轨迹方程,得到为:x2+y2+xy=1
故曲线Γ的方程是椭圆,其焦点坐标为F1(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$,),F2($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$).
点评 本题主要考查直线和圆的位置关系的判断及其运用,以及曲线轨迹方程的求法,直线与椭圆的位置关系的应用,椭圆的基本知识的应用和对称性的问题,综合性强,计算量大,化简难度高,要从所学的知识点出发来证明.属于难题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{5}$ | C. | $-\frac{2}{5}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (±1,0) | B. | (±2,0) | C. | $(±2\sqrt{2},0)$ | D. | (±4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π,x=$\frac{kπ}{2}$(k∈Z) | B. | $\frac{π}{2}$,x=kπ(k∈Z) | C. | π,x=kπ(k∈Z) | D. | $\frac{π}{2}$,x=$\frac{kπ}{2}$(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com