
分析 三角形的边长为正数,而且任意两边之和大于第三边才能构成三角形,故只需求出函数在区间[0,2]上的最小值与最大值,从而可得不等关系,即可求解.
解答 解:f(x)=x3-3x+m,求导f'(x)=3x2-3,由f'(x)=0得到x=1或者x=-1,
又x在[0,2]内,∴函数f(x)在区间(0,1)单调递减,在区间(1,2)单调递增,
则f(x)min=f(1)=m-2,f(x)max=f(2)=m+2,f(0)=m.
在[0,2]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边的三角形,
三个不同的数a,b,c对应的f(a),f(b),f(c)可以有两个相同.
由三角形两边之和大于第三边,可知最小边长的二倍必须大于最大边长.
由题意知,f(1)=-2+m>0…(1),
f(1)+f(1)>f(0),得到-4+2m>m…(2),
f(1)+f(1)>f(2),得到-4+2m>2+m…(3),
由(1)(2)(3)得到m>6为所求.
故答案为:(6,+∞).
点评 本题以函数为载体,考查构成三角形的条件,解题的关键是求出函数在区间[0,2]上的最小值与最大值.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x${\;}^{\frac{1}{2}}$ | B. | y=$\frac{1}{{x}^{2}}$ | C. | y=x${\;}^{-\frac{1}{2}}$ | D. | y=$\sqrt{2}$x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a | B. | -a | C. | ±a | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 12π | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
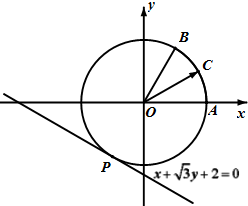 如图,圆O与直线x+$\sqrt{3}$y+2=0相切于点P,与x正半轴交于点A,与直线y=$\sqrt{3}$x在第一象限的交点为B.点C为圆O上任一点,且满足$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,以x,y为坐标的动点D(x,y)的轨迹记为曲线Γ.
如图,圆O与直线x+$\sqrt{3}$y+2=0相切于点P,与x正半轴交于点A,与直线y=$\sqrt{3}$x在第一象限的交点为B.点C为圆O上任一点,且满足$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,以x,y为坐标的动点D(x,y)的轨迹记为曲线Γ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$π | B. | 5π | C. | 4π | D. | $\frac{5}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | y=±4x | D. | y=±$\frac{1}{4}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com