Question

20．在凸四边形ABCD中，角A=C=60°，AD=BC=2，且AB≠CD，则四边形ABCD的面积为$\sqrt{3}$．

Answer 1

分析 设AB=x，CD=y（x≠y），连接BD，在△ABD和△BCD中，运用余弦定理，化简可得x+y=2，再由四边形ABCD的面积为△ABD和△BCD的面积之和，运用三角形的面积公式，计算即可得到所求．

解答 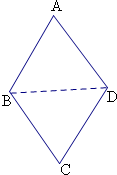解：设AB=x，CD=y（x≠y），
连接BD，在△ABD中，BD²=x²+2²-2×2•xcos60°，
在△BCD中，BD²=y²+2²-2×2•ycos60°，
所以x²+2²-2×2•xcos60°=y²+2²-2×2•ycos60°，
即（x-y）（x+y-2）=0，所以x+y=2，
所以$S={S_{△ABD}}+{S_{△BCD}}=\frac{1}{2}×2•xsin{60°}+\frac{1}{2}×2•ysin{60°}$=$\frac{{\sqrt{3}}}{2}（x+y）=\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题考查四边形的面积的求法，注意运用分割思想和三角形的面积公式，同时考查三角形的余弦定理，属于中档题．