
分析 (1)把a=4代入函数g(x)的解析式,求出导数,得到g(0)和g′(0),由直线方程的点斜式得切线方程;
(2)利用导数求出函数f(x)在[t,t+2]上的单调区间,求出极值和区间端点值,比较大小后得到f(x)在区间[t,t+2](t>0)上的最小值;
(3)把f(x)和g(x)的解析式代入g(x)=2exf(x),分离变量a,然后构造函数$h(x)=x+2lnx+\frac{3}{x}$,由导数求出其在[$\frac{1}{e}$,e]上的最大值和最小值,则实数a的取值范围可求.
解答 解:(Ⅰ)当a=4时,g(x)=(-x2+4x-3)ex,g(0)=-3.
g′(x)=(-x2+2x+1)ex,故切线的斜率为g′(0)=1,
∴切线方程为:y+3=x-0,即y=x-3;
(Ⅱ)f′(x)=lnx+1,
| x | $(0,\frac{1}{e})$ | $\frac{1}{e}$ | $(\frac{1}{e},+∞)$ |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值(最小值) | 单调递增 |
| x | $(\frac{1}{e},1)$ | 1 | (1,e) |
| h′(x) | - | 0 | + |
| h(x) | 单调递减 | 极小值(最小值) | 单调递增 |
点评 本题考查了导数在求函数最值中的应用,关键在于由导函数的符号确定原函数的单调性,考查利用构造函数法求解含字母系数的范围问题,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 91.5和91.5 | B. | 91.5和92 | C. | 91和91.5 | D. | 92和92 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为半圆O的直径,AD⊥AB,过D作圆的另一切线DC交AB的延长线于E,C为切点,连接BC,OD.
如图,AB为半圆O的直径,AD⊥AB,过D作圆的另一切线DC交AB的延长线于E,C为切点,连接BC,OD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
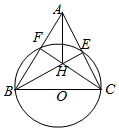 如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:
如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
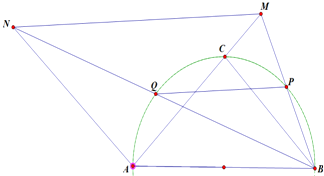 如图,在以AB为直径的半圆上有三点P,C,Q,且∠CBA=∠PBQ=45°,BP与AC交于点M,过点M作PQ的平行线,交BQ于点N.
如图,在以AB为直径的半圆上有三点P,C,Q,且∠CBA=∠PBQ=45°,BP与AC交于点M,过点M作PQ的平行线,交BQ于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com