【答案】
分析:(1)利用a
1=0时,且对任意k∈N
*,a
2k-1,a
2k,a
2k+1成等差数列,代入计算,可求a
2,a
3,a
4;
(2)观察已知条件可得a
2k+1-a
2k-1=4k,利用累加法a
2k+1=a
1+(a
3-a
1)+(a
5-a
3)+…+(a
2k-1+a
2k-3)可求出a
2k+1,从而可得数列的通项;
(3)确定数列的通项,利用分组求和法,即可证得结论.
解答:(1)解:由题设,可得a
2=a
1+2=2,a
3=a
2+2=4,a
4=a
3+4=8;
(2)解:由题意可得a
2k+1-a
2k-1=4k,k∈N
+,
所以a
2k+1-a
1=(a
2k+1-a
2k-1)+(a
2k-1-a
2k-3)+…+(a
3-a
1)=4k+4(k-1)+…+4×1=2k(k+1)
由a
1=0,得a
2k+1=2k(k+1),从而a
2k=a
2k+1-2k=2k
2,a
2k+2=2(k+1)
2于是数列{a
n}的通项公式为
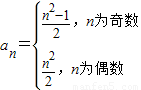
;
(3)证明:由(2)知,当n为偶数时,
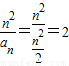
当n为奇数时,
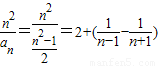
n=2时,2n-T
n=4-2=2,不等式成立
当n为偶数且n≥4时,
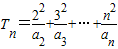
=
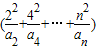
+
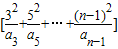
=
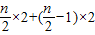
+
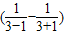
+…+[
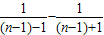
]=2n-2+
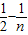
=
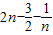
∴
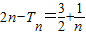
∴
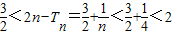
综上,当n为偶数时,有
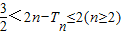
.
点评:本题主要考查等差数列的定义及通项公式,前n项和公式、等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法.

 ,证明:当n为偶数时,有
,证明:当n为偶数时,有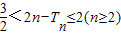 .
.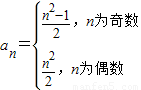 ;
;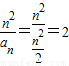
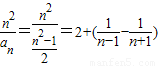
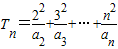 =
=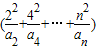 +
+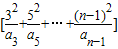
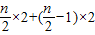 +
+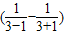 +…+[
+…+[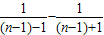 ]=2n-2+
]=2n-2+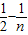 =
=
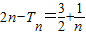
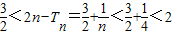
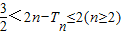 .
.
