练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知a，b，c分别为△ABC三个内角A，B，C所对的边长，且acosB﹣bcosA= c．
    （1）求 的值；
    （2）若A=60°，求 的值．

    【答案】
    （1）解：△ABC中，由条件利用正弦定理 ，

    可得sinAcosB﹣sinBcosA= sinC．

    又sinC=sin（A+B）=sinAcosB+cosAsinB，所以， sinAcosB= sinBcosA，

    可得 = ．


    （2）解：若A=60°，则tanA= ，得tanB= ．

    ∵cosC= ，

    ∴ = =﹣ tan（A+B）= =﹣


    【解析】（1）△ABC中，由条件利用正弦定理可得sinAcosB﹣sinBcosA= sinC．又sinC=sin（A+B）=sinAcosB+cosAsinB，可得 sinAcosB= sinBcosA，由此可得 的值．（2）可求tanA= ，由（1）得tanB= ．利用余弦定理，两角和的正切函数公式即可化简求值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知一组数据x1 ， x2 ， x3 ， x4 ， x5的平均数是2，方差是 ，那么另一组数据2x1﹣1，2x2﹣1，2x3﹣1，2x4﹣1，2x5﹣1的平均数，方差分别是（ ）
    A.3，
    B.3，
    C.4，
    D.4，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面向量 、 满足| |=| |=1， = ，若向量 满足| ﹣ + |≤1，则| |的最大值为（ ）
    A.1
    B.
    C.
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的前三项依次为a﹣2，a+2，a+8，则an=（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）求函数f（x）= （x＜﹣1）的最大值，并求相应的x的值．
    （2）已知正数a，b满足2a2+3b2=9，求a 的最大值并求此时a和b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥P﹣ABC中，PA⊥平面ABC，AB=BC=AC=2，PA= ，E，F分别是PB，BC的中点，则EF与平面PAB所成的角等于（ ）
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， 设an是Sn与2的等差中项，数列{bn}中，b1=1，点P（bn ， bn+1）在直线y=x+2上．
    （1）求an ， bn；
    （2）若数列{bn}的前n项和为Bn ， 比较 + +…+ 与1的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为（ ）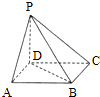
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

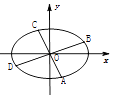
    【题目】已知椭圆 的离心率为 ，且过点 ．
    （1）求椭圆的标准方程；
    （2）四边形ABCD的顶点在椭圆上，且对角线AC、BD过原点O，若 ． （i） 求 的最值；
    （ii） 求四边形ABCD的面积．

    查看答案和解析>>

    同步练习册答案