
在二项式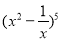 的展开式中,含
的展开式中,含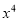 的项的系数是( )
的项的系数是( )
A.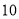 B.
B. C.
C.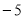 D.
D.
科目:高中数学 来源:2015届广东省梅州市高二下学期期中文科数学试卷(解析版) 题型:填空题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心( ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期中文科数学试卷(解析版) 题型:填空题
将石子摆成如下图的梯形形状.称数列 为“梯形数”.根据图形的构成,判断数列的第
为“梯形数”.根据图形的构成,判断数列的第 项
项 ______________;
______________;

查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高三第一次调研考试理科数学试卷(解析版) 题型:解答题
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1) 求 的值;
的值;
(2) 根据样本数据,试估计这一年度的空气质量指数的平均值;(注:设样本数据第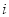 组的频率为
组的频率为 ,第
,第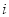 组区间的中点值为
组区间的中点值为
 ,则样本数据的平均值为
,则样本数据的平均值为 .)
.)
(3) 如果空气质量指数不超过 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高三第一次调研考试文科数学试卷(解析版) 题型:填空题
已知在平面直角坐标系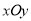 中圆
中圆 的参数方程为:
的参数方程为: ,(
,(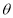 为参数),以
为参数),以 为极轴建立极坐标系,直线极坐标方程为:
为极轴建立极坐标系,直线极坐标方程为: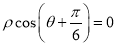 ,则圆
,则圆 截直线所得弦长为 .
截直线所得弦长为 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高二3月月考理科数学试卷(解析版) 题型:解答题
已知函数 ,且
,且 是函数
是函数 的一个极小值点.
的一个极小值点.
(1)求实数 的值;
的值;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2015届广东省等六校高三8月联考文科数学试卷(解析版) 题型:解答题
某体育杂志针对2014年巴西世界杯发起了一项调查活动,调查“各球队在世界杯的名次与该队历史上的的实力和表现有没有关系”,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| 有关系 | 无关系 | 不知道 |
40岁以下 | 800 | 450 | 200 |
40岁以上(含40岁) | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从持“有关系”态度的人中抽取45人,求n的值,并求从持其他两种态度的人中应抽取的人数;
(2)在持“不知道”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任选取2人,求至少一人在40岁以下的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com