
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1) 求 的值;
的值;
(2) 根据样本数据,试估计这一年度的空气质量指数的平均值;(注:设样本数据第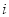 组的频率为
组的频率为 ,第
,第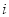 组区间的中点值为
组区间的中点值为
 ,则样本数据的平均值为
,则样本数据的平均值为 .)
.)
(3) 如果空气质量指数不超过 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.

(1)0.03;(2)24.6;(3)分布列详见解析, .
.
【解析】
试题分析:本题主要考查频率分布直方图、由样本估计总体求平均值、二项分布、离散型随机变量的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力、计算能力、转化能力.第一问,利用频率分布直方图中长方形的高=频率/组距,而所有频率之和为1,来计算a的值;第二问,根据样本数据,估计总体的平均值的计算公式为:频率分布直方图中,每一个长方形的中点×高×组距,得到的数据之和即为平均值;第三问,利用频率分布直方图先得到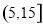 内的频率,即“特优等级”的概率值,通过分析题意可知随机变量
内的频率,即“特优等级”的概率值,通过分析题意可知随机变量 服从二项分布,利用
服从二项分布,利用 计算出每一种情况的概率,再利用
计算出每一种情况的概率,再利用 计算出数学期望
计算出数学期望 .
.
试题解析:(1) 由题意,得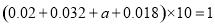 , 1分
, 1分
解得 . 2分
. 2分
(2) 个样本中空气质量指数的平均值为
个样本中空气质量指数的平均值为
 3分
3分
由样本估计总体,可估计这一年度空气质量指数的平均值约为 . 4分
. 4分
(3)利用样本估计总体,该年度空气质量指数在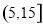 内为“特优等级”,
内为“特优等级”,
且指数达到“特优等级”的概率为 ,则
,则 . 5分
. 5分
 的取值为
的取值为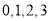 , 6分
, 6分
 ,
, ,
,
 ,
, . 10分
. 10分
∴ 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
11分
∴ . 12分
. 12分
(或者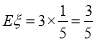 )
)
考点:频率分布直方图、由样本估计总体求平均值、二项分布、离散型随机变量的分布列和数学期望.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2015届广东省梅州市高二下学期期中理科数学试卷(解析版) 题型:选择题
如图A、B、C、D是某油田的四口油井,计划建三条路,将这四口油井连结起来(每条路只连结两口油井),那么不同的建路方案有 ( )

A.12种 B.14种 C.16种 D.18种
查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高二3月月考文科数学试卷(解析版) 题型:选择题
在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若 的观测值为
的观测值为 ,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误
D.以上三种说法都不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com